Appendix: Infinity
You probably have never given much thought to characterising infinity other
than the recognition that there is no end to it. Infinite quantities can be
discomfitting, and most applications of mathematics shy away from dealing with
them. You may be surprised to learn that there are several sizes of infinity.
(In fact, there is an infinite number of them.) In order to see this, we must
examine the way in which we compute sizes of finite sets and see how it
generalises to the infinite case.
What is the size of the set maddabaybie, snoo, updok? How did you get that
answer? You counted. The process of counting is an act of putting the
elements of a set into one-to-one correspondence with a sequence of natural
numbers 1, 2, 3, .... The last number in the sequence is the number of
elements in the set. The natural numbers, therefore, are nothing but abstract
properties of sets of objects. A couple of lovers and a pair of socks are both
instances of the number two, because they both can be mapped in a one-to-one
manner to the set 1, 2. Any finite set can have its elements marked off like
this, placed in a one-to-one correspondence with a sequence of natural numbers.
If this can be done for any finite set, it is natural to ask whether the
definition of number can be extended so that there are numbers that describe
infinite sets, for there do exist one-to-one correspondences that map between
infinite sets.
Often it is easier to show that two sets are the same size than to specify the
particular size that they have in common. Russell[50] uses
the example of the relationship between husbands and wives. The relationship,
marriage, constitutes a one-to-one mapping between the set of husbands and the
set of wives. (We assume for the sake of this example that there is no
polygamy.) Since there is exactly one husband for each wife, and exactly one
wife for each husband, it can be inferred that the set of wives and the set of
husbands have the same size. Thus if we know the size of the set of wives,
then we also know the size of the set of husbands, and vice versa. In this
example, the size is finite. But it need not be so.
The simplest infinity is countable infinity or enumerable infinity.
The members of a countably infinite set can be counted. That is, it is
possible to place them in one-to-one correspondence with the natural
numbers--not a finite sequence of natural numbers, not just a part of the set
of natural numbers, but all the natural numbers. All the sets that can
be placed into one-to-one correspondence with the natural numbers share the
property of countability. The natural numbers 0, 1, 2, 3, ... are of course
countable, because any set can be placed in one-to-one correspondence with
itself. So are the integers 0, 1, -1, 2, -2, 3, -3, .... Another term for the
size of a set is cardinality. The cardinality of a finite set of size
n is just the number n. The cardinality of a countably infinite
set is 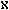 0. (`
0. (`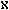 ' is aleph, the first letter of the Hebrew
alphabet. `
' is aleph, the first letter of the Hebrew
alphabet. `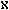 0' is read "aleph-null".)
0' is read "aleph-null".) 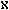 0 is a cardinal
number. You have probably been taught (or perhaps you will yet be taught)
in your mathematics classes that it is a mistake to treat infinity as a number.
This is true in the context of arithmetic on the real or complex numbers. But
numeration can be extended to infinite quantities; it is only a matter of
making consistent definitions. Infinite cardinal numbers do not obey the same
algebraic rules as finite numbers. For example, there is no distributive
property;
0 is a cardinal
number. You have probably been taught (or perhaps you will yet be taught)
in your mathematics classes that it is a mistake to treat infinity as a number.
This is true in the context of arithmetic on the real or complex numbers. But
numeration can be extended to infinite quantities; it is only a matter of
making consistent definitions. Infinite cardinal numbers do not obey the same
algebraic rules as finite numbers. For example, there is no distributive
property; 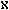 0+
0+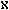 0 =
0 = 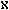 0. (Think of the cardinality of the
natural numbers in comparison with that of the integers.) The only distinction
that will be made between types of infinity here is the distinction between
countable and uncountable infinity.
0. (Think of the cardinality of the
natural numbers in comparison with that of the integers.) The only distinction
that will be made between types of infinity here is the distinction between
countable and uncountable infinity.
The rational numbers are also countable, but this proof takes more work. The
rational numbers are the numbers that can be expressed as quotients of
integers. They can be generated in an infinite matrix whose rows and columns
are labelled with the generating integers. The column number is the numerator,
and the row number is the denominator.
0 1 -1 2 -2 3 -3 ...
1 0/1 1/1 -1/1 2/1 -2/1 3/1 -3/1 ...
-1 0/-1 1/-1 -1/-1 2/-1 -2/-1 3/-1 -3/-1 ...
2 0/2 1/2 -1/2 2/2 -2/2 3/2 -3/2 ...
-2 0/-2 1/-2 -1/-2 2/-2 -2/-2 3/-2 -3/-2 ...
3 0/3 1/3 -1/3 2/3 -2/3 3/3 -3/3 ...
-3 0/-3 1/-3 -1/-3 2/-3 -2/-3 3/-3 -3/-3 ...
: : : : : : : :
Obviously, there are many duplicate values constructed by this table, but these
can be excluded in the enumeration. At any particular point in the
enumeration, the list of rationals built up so far is finite, so it can be
searched in finite time. The value of the ratio currently under consideration
can be compared with all the values in the list, and added to the list if and
only if it is not already present. All that remains is to specify an order in
which to consider all the ratios in the table. Here is one.
Therefore the rationals are countably infinite. We can think of taking this
squiggly line (ray, actually) that touches all the rationals, removing
duplicates from it, and stretching it out so that it looks just like the
natural number line.
The matrix used above to generate the rationals can be extended to infinity in
all directions and viewed as a 2-space of integers. An enumeration scheme can
be constructed to spiral outward from the origin in such a 2-space. Such an
enumeration will eventually reach any coördinate in the space. Therefore,
the set of the integer pairs in 2-space is of cardinality 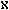 0. An
enumeration scheme can be constructed for any number of dimensions. Therefore,
the cardinality of the integer tuples in n-space, for all n, is
0. An
enumeration scheme can be constructed for any number of dimensions. Therefore,
the cardinality of the integer tuples in n-space, for all n, is
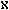 0.
0.
So far the only property that we have proven about an infinite set is
countability. Uncountability can also be proven. One common way of proving a
set uncountable is Cantor diagonalisation, devised by Georg Cantor.
Cantor diagonalisation is an indirect proof method; it supposes that the set in
question is countable, and therefore that all the elements of the set can be
included in an enumeration, and uses that assumption to construct a way of
specifying for every possible enumeration an element that is in the set but is
not included in the enumeration. The real numbers in the interval (0, 1) are
uncountably infinite. To see that this is so, suppose that the reals in (0, 1)
are countable. Then there must be some enumeration of all of them. Here is
one possible enumeration:
0.042546...
0.583901...
0.839702...
0.043850...
0.374508...
0.572947...
:
This list can be viewed as a matrix, with the row index representing the
position in the enumeration and the column index representing the decimal
place. Observe the decimal generated by the diagonal of this matrix. A number
that is not included in the enumeration can be generated by altering every
digit on the diagonal. A number constructed in this way differs from the
i[th] number in the enumeration in the i[th] decimal place. The example above cannot be a complete
enumeration, because there is some number 0.190918... that is not included in
it. This construction is valid for any proposed enumeration. Suppose an
adversary in this argument says, "Well, if that number 0.190918... isn't in my
enumeration, I'll just stick it in." The adversary is still no closer to
constructing an enumeration of all the reals in (0, 1), because we can take the
new enumeration, which includes 0.190918..., and use the same method as before
to construct another number that is not included in it. No matter how many
holes the adversary patches, there will always be more. Therefore, the reals
are uncountable. The cardinality of the reals is denoted c. Obviously,
c is greater than 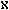 0.
0.
Two sets are of the same cardinality, whether that cardinality is finite or
infinite, if and only if a one-to-one mapping between all their elements can be
constructed. Thus the set of all integers is the same size as the set of all
natural numbers:
0 1 2 3 4 5 6 ...
0 1 -1 2 -2 3 -3 ...
The one-to-one function here from any natural number n to any integer
k is
n odd -> (n+1)/2
[] n even -> -n/2
Since this definition of equivalent size applies to infinite sets, it can be
used to show that the cardinality of all the real numbers is the same as the
cardinality of the reals in the interval (0, 1). Consider the function
y = tan(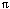 .(x-1/2)) on the interval (0, 1), which has
asymptotes at x=1 and at x=0 and constitutes a one-to-one mapping
from the reals in (0, 1) to all the reals.
(If you have not yet studied trigonometry, you will learn about the tangent
function when you do. How it arises and what it is used for are not germane to
this discussion; it is sufficient that it exists and is a mapping from (0, 1)
to
.(x-1/2)) on the interval (0, 1), which has
asymptotes at x=1 and at x=0 and constitutes a one-to-one mapping
from the reals in (0, 1) to all the reals.
(If you have not yet studied trigonometry, you will learn about the tangent
function when you do. How it arises and what it is used for are not germane to
this discussion; it is sufficient that it exists and is a mapping from (0, 1)
to 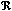 .)
.)
The reals in the plane are of the same cardinality, c, as the reals on
a line. A one-to-one correspondence between these two domains can be defined
by interleaving the digits of a pair of coördinates. Any real number can
be represented in decimal notation by a string of the form x.y, where
x and y are the digit strings representing the integral part and
the fractional part, respectively, of the the real number. Let xi
denote the i[th ]digit in the string x.
Then a one-to-one correspondence can be created by encoding the pair of
reals (u.v, x.y) in the single real
u0x0u1x1...u|u|-1x|x|-1 .
v0y0v1y1...v|v|-1y|y|-1. This scheme interleaves
the two integral parts and the two fractional parts separately and thereby
preserves information on the location of the decimal point within each
coördinate. (Numbers can be padded with 0's on the left and on the right,
if necessary, to make both numbers contain the same number of digits.) Take a
moment to think for yourself how this encoding scheme can be generalised to
coördinates in n-space.
The complex numbers are all the numbers of the form a+bi, where
i is the imaginary number 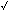 -1. Since the complex numbers may
be viewed as pairs of reals (a, b), they have the same cardinality as
the reals in the plane, namely, c.
-1. Since the complex numbers may
be viewed as pairs of reals (a, b), they have the same cardinality as
the reals in the plane, namely, c.
[50][Russell 1920]
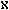 0. (`
0. (`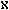 ' is aleph, the first letter of the Hebrew
alphabet. `
' is aleph, the first letter of the Hebrew
alphabet. `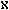 0' is read "aleph-null".)
0' is read "aleph-null".) 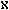 0 is a cardinal
number. You have probably been taught (or perhaps you will yet be taught)
in your mathematics classes that it is a mistake to treat infinity as a number.
This is true in the context of arithmetic on the real or complex numbers. But
numeration can be extended to infinite quantities; it is only a matter of
making consistent definitions. Infinite cardinal numbers do not obey the same
algebraic rules as finite numbers. For example, there is no distributive
property;
0 is a cardinal
number. You have probably been taught (or perhaps you will yet be taught)
in your mathematics classes that it is a mistake to treat infinity as a number.
This is true in the context of arithmetic on the real or complex numbers. But
numeration can be extended to infinite quantities; it is only a matter of
making consistent definitions. Infinite cardinal numbers do not obey the same
algebraic rules as finite numbers. For example, there is no distributive
property; 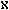 0+
0+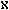 0 =
0 = 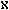 0. (Think of the cardinality of the
natural numbers in comparison with that of the integers.) The only distinction
that will be made between types of infinity here is the distinction between
countable and uncountable infinity.
0. (Think of the cardinality of the
natural numbers in comparison with that of the integers.) The only distinction
that will be made between types of infinity here is the distinction between
countable and uncountable infinity.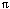 .(x-1/2)) on the interval (0, 1)
.(x-1/2)) on the interval (0, 1)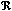 .)
.)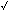 -1. Since the complex numbers may
be viewed as pairs of reals (a, b), they have the same cardinality as
the reals in the plane, namely, c.
-1. Since the complex numbers may
be viewed as pairs of reals (a, b), they have the same cardinality as
the reals in the plane, namely, c.