2
Language
You taught me language; and my profit on't
Is, I know how to curse. The red plague rid you
For learning me your language!
--Caliban (The Tempest 1.2.363-365)
'Tis but thy name that is my enemy;
Thou art thyself, though not a Montague.
What's Montague? It is nor hand, nor foot,
Nor arm, nor face, nor any other part
Belonging to a man. O, be some other name!
What's in a name? That which we call a rose
By any other word would smell as sweet...
--Juliet (Romeo and Juliet 2.2.38-44)
Lewis Carroll: Mathematics in Literature
In 1851, three years before Boole published The Laws of Thought,
Charles Lutwidge Dodgson entered Oxford University. As an undergraduate,
Dodgson distinguished himself in mathematics. After taking his degree, he
spent the rest of his life at Oxford. As a mathematician he was mediocre. He
wrote prolifically on mathematics, but his conservatism went against the grain
of the mathematical innovation of the nineteenth century. His mathematical
texts were never significant and are read now only because of historical
interest. One point of interest in them, however, is the fascination with
notation that they display. In his 1861 pamphlet The Formulae of Plane
Trigonometry, for example, he introduced new symbols for the trigonometric
functions. These were pictograms that attempted to express the nature of the
functions, rather than the textual abbreviations (`sin', `cos', `tan', `sec',
&c.) that were, and still are, the convention. Dodgson interested himself
in logic and must have read and been influenced by the work of Peacock and
later that of Boole.
Dodgson enjoyed the company of little girls. It feels likely to me that a
factor in this tendency was an appreciation of the native state of the human
mind, of the child's natural sense of wonder, the same sense revealed in To
the Lighthouse. Dodgson enjoyed amusing his child friends with games of
logic and wordplay. A favourite child friend of Dodgson's was Alice Liddell,
the daughter of the dean of his college at Oxford. On July 4, 1862, Dodgson
and a colleague accompanied her and her two sisters on a rowing trip up the
River Isis near Oxford. On the way, Dodgson made up a story to amuse the
girls. Alice later prevailed upon Dodgson to write down the tale. Dodgson is
better known by his pseudonym, Lewis Carroll, for this work, which became
Alice's Adventures in Wonderland (1865). The conundrums and absurdities
of Wonderland, and of the looking-glass world in Through the Looking Glass
(1871), are metaphor for a child's everyday encounters with the universe.
A full commentary on the works of Lewis Carroll, or even just on Alice's
Adventures in Wonderland, would be a heavy tome. So we must restrict
ourselves here to a few (arbitrarily selected) points illustrating the
(omni)presence of nineteenth-century abstract algebraic thought in Carroll's
work. We have seen that by the time Carroll began writing, the English
algebraists had removed inherent meaning from algebraic symbols. Alice's fall
down the rabbit hole in the beginning of Alice's Adventures in Wonderland
is packed with images of symbols as arbitrarily defined markers, labels,
and mechanically applied rules of inference. Just before she sees the white
rabbit, she peeps at the book that her sister is reading, and thinks, "What is
the use of a book without pictures or conversations?"[26]
From within Alice's system of understanding, that of a seven-year-old girl in
Victorian England, such a book is useless; she can't get any meaning out of it.
As Alice falls, she passes "cupboards and bookshelves" filled with curiosities.
Among them are "maps and pictures hung upon pegs". A map, of course, is an
arbitrary encoding of a geographical area, just as an algebraic symbol is an
arbitrary encoding. Carroll returns to the subject of maps in other writings.
In Through the Looking Glass, there is the idea of a map of unit scale,
so large that it covers exactly the country that it represents. In
mathematical terms, Carroll has taken the one-to-one correspondence of map and
terrain and made it an identity function. This transformation is a perfectly
sound one in the domain of abstract mathematics, but when connected with
physical reality it becomes ludicrously impractical. In The Hunting of the
Snark, Carroll returns to the idea of an absurd map and makes the connexion
with abstract algebra even more explicit. The following passage is from the
second fit, a characterisation of the Bellman, the leader of the Snark hunting
expedition:
He had bought a large map representing the sea,
Without the least vestige of land:
And the crew were much pleased when they found it to be
A map they could all understand.
"What's the good of Mercator's North Poles and Equators,
Tropics, Zones, and Meridian Lines?"
So the Bellman would cry: and the crew would reply
"They are merely conventional signs!
"Other maps are such shapes, with their islands and capes!
But we've got our brave captain to thank"
(So the crew would protest) that he's bought us the best--
A perfect and absolute blank!"[27]
Note Carroll's careful choice of words. The map represents the sea.
The specification that the Bellman bought the map adds comedy.
Objectively, he would have been just as well off with a blank sheet of paper,
or with no paper at all. But the act of buying the map has made the blank
sheet a map in the mind of the Bellman and his crew. Map symbols such as
latitudes and longitudes are indeed arbitrary divisions, "conventional signs"
like the symbols of abstract algebra. There are many other instances of play
with labellings and encodings in Carroll's works, but I shall leave you with
the excuse that they are best left for the reader to discover. That is, after
all, the play of it.
The Hunting of the Snark also contains an instance of the falling into
superfluity that I have mentioned as a consequence of the Information Age:
Then the Butcher contrived an ingenious plan
For making a separate sally;
And had fixed on a spot unfrequented by man,
A dismal and desolate valley.
But the very same plan to the Beaver occurred:
It had chosen the very same place:
Yet neither betrayed, by a sign or a word,
The disgust that appeared in his face.[28]
This is a metaphor for what had already begun in Dodgson's time. The Butcher
has specialised; he has found his niche, "a spot unfrequented by man, / A
dismal and desolate valley". When scholars Butcher and Beaver finally learn of
each other's work, they find that they have been duplicating each other's
efforts, but they conceal their disappointment. Maybe they can publish a joint
paper on their method of hunting the Snark. If they do, one would hope that
their proof would be mathematically rigorous, and not in the Bellman's style.
For according to the Bellman, all that he has to do in order to prove a
proposition is to state it three times in different ways. How many papers have
you read (or written, at three o'clock in the morning on the night before it
was due) that try to use this method to fudge and to escape logical rigour?
"Just the place for a Snark! I have said it thrice: / What I tell you three
times is true."[29] Unfortunately, the Butcher, who is a
bit dim, puts his faith in the Bellman's misleading sophistry:
"'Tis the voice of the Jubjub!" he suddenly cried.
(This man, that they used to call "Dunce.")
"As the Bellman would tell you," he added with pride,
"I have uttered that sentiment once.
"`Tis the note of the Jubjub! Keep count, I entreat.
You will find I have told it you twice.
'Tis the song of the Jubjub! The proof is complete.
If only I've stated it thrice."[30]
This reference to the fall into superfluity is especially potent, embedded as
it is among references to abstract algebra. For, as already noted, abstract
algebra seems to have come over the entire Cambridge mathematical community at
once.
Mock judicial proceedings are fertile ground for Dodgson. Legal language is
natural language trying to behave as a formal system. Systems of law are
fundamentally imperfect attempts to capture moral feelings of right and wrong
in black marks on paper. The Snark hunting expedition has brought along a
Barrister, "to arrange [the crew's] disputes". The sixth fit of The Hunting
of the Snark comprises a dream of the Barrister in which the Snark is
"defending a pig / On the charge of deserting its sty." The dream contains
Carroll's indictment (so to speak) of legal finagling and the too-serious
application of legal systems:
The indictment had never been clearly expressed,
And it seemed that the Snark had begun,
And had spoken three hours, before any one guessed
What the pig was supposed to have done.[31]
Alice's introduction to legal systems occurs in chapter eleven of Alice's
Adventures in Wonderland. From her external point of view, it seems that
the legal system encompasses not only laws, but also, more potently, behaviour
in the court--or should I say, courtly behaviour. She identifies the judge
"because of his great wig", a symbol that she recognises as signifying
judgeship. The trial of the knave is an occasion for redefinition of terms,
wordplay, and comic misinterpretation.
A fascination with symbolisation is a feature occurring in the lives of many
scientists and mathematicians, especially in their childhoods. To take one
contemporary example: The physicist Richard Feynman wrote in his
autobiographical work Surely You're Joking, Mr. Feynman! of his
invention of new symbols that seemed more reasonable to him when doing
calculus. Since nobody else could understand this private scheme of
abbreviation, Feynman eventually discarded it and began to use conventional
notation. When I was learning calculus, in the eleventh grade in a suburban
public high school, my own play with symbols was the source of some woe for my
teacher. I could not bring myself to use the symbol `=' in substitutions of
variables. If a new variable u were being introduced, I thought, it
felt uncomfortable to treat it just like one of the pre-existing parameters of
the problem by using `='. There should be some clue or mnemonic in the
notation that would signify that such a variable was being defined, not merely
expressed. So I borrowed the `:=' assignment symbol from the computer
programming language Pascal and used it in substitions of variables in my
calculus proofs. I also put slashes through my zeroes, as some computer
character sets do, because I disliked the orthographical ambiguity between the
numeric symbol `0' and the letter `O'. I was naïvely striving for a
universal semeiotics, a set of symbols that would apply in all contexts.
Dodgson composed the first stanza of "Jabberwocky", the famous mirror-image
nonsense poem in Through the Looking Glass, in 1855, when he was
twenty-three:
Twas bryllyg, and the slythy toves
Did gyre and gymble in the wabe:
All mimsy were the borogoves;
and the mome raths outgrabe.
Significantly, he first conceived of this not as nonsense in everyday Modern
English, but as Anglo-Saxon nonsense. But being nonsense, how can nonsense be
in any particular language? Often we can recognise a foreign language by its
sound, even if we do not know the language. Natural languages have distinctive
sounds. Douglas Hofstadter presents some fascinating discussions of this idea
of spirits or essences of particular languages in his collection of essays
Metamagical Themas. This first stanza of "Jabberwocky" is easily read
in Old English, with some syntactic translations, whereas portions of the rest
of the poem, conceived of as Modern English nonsense, produce phonetic
difficulties. Did you ever read a Tom Swift or Hardy Boys book in which
somebody (Biff Hooper, perhaps) "chortled"? When Dodgson used this word in
"Jabberwocky", it was just another of his many nonsense terms. But,
ironically, the popularity of this particular piece of nonsense, along with the
context in which the word occurred ("He chortled in his joy") has caused
"chortled" to become a bona fide term in the English language, meaning a
kind of laughing. The Anglo-Saxon appears briefly also in the seventh chapter
of Through the Looking Glass, with the Anglo-Saxon messenger, Carroll's
spoof on Anglo-Saxon scholarship. In the eighth chapter, the Anglo-Saxon is
replaced, following historical developments, with the chivalric encounter of
the White Knight and the Red Knight. Before having ado with the Red Knight,
the White Knight mentions "the Rules of Battle". While they fight, Alice is
left wondering what the Rules of Battle are, and trying to determine them
empirically. Chivalry is a system foreign to Alice, so she has no intuition
for its rules.
Puns have been around since prehistory. Punning comes as naturally to humans
as telling jokes. But it was Dodgson who elevated wordplay from the status of
a mere curiosity, a basis for cheap one-liners, and based works of literature
on it. Dodgson's was the first literature to rely heavily on portmanteau
words, words that use the human tendency toward analogy in phonetics, spelling,
visual presentation, historical and cultural referents--every possible
container for information--to overload single terms with multiple meanings.
The portmanteau word would have entered literature without the work of Dodgson;
after the new algebra of the nineteenth century and its parent philosophy of
language, it was inevitable that what has come to be termed "semeiotics", the
study of symbols, would become more explicit in literature just as it had in
the sciences. James Joyce invented the concept independently of Dodgson, and
when he began to publish his experimentation with the technique, people told
him that it reminded them of the work of Lewis Carroll, whom he had never read
at that point.[32] Finnegans Wake, Joyce's
masterpiece of multiple semantics, contains several references to Lewis
Carroll, among them an acknowledgement of Dodgson's priority: "To tell how your
mead of, mard, is made of. All old Dadgerson's dodges one conning one's
copying and that's what wonderland's wanderlad'll flaunt to the fair."[33] [Atherton 1960] contains a discussion of this and other
references to Carroll in Finnegans Wake and of the influence in general
of Carroll on Joyce. Dodgson often played his game of "doublets" with his
child friends, in which the objective is to transform one word into another by
making a series of words in which one letter is changed at each step in the
series. The first sentence in the above quotation is Joyce's variant of
doublets. The phrase "Dadgerson's dodges" needs no explaining.
Before leaving the subject of Lewis Carroll, I must remark upon the presence
in his work of a certain number that had no distinction in his day but recently
has become well known because of its appearance in the work of another author.
Whenever Carroll needed some arbitrary number, it seems, he chose forty-two.
In chapter twelve of Alice's Adventures in Wonderland, the King, during
the trial of the Knave, produces "Rule forty-two. All persons more than a
mile high to leave the court."[34] The Baker in The
Hunting of the Snark came with forty-two boxes. In his preface to
The Hunting of the Snark, Carroll explains that the Bellman "would only
refer to his Naval Code"--this is the system within which the Bellman exists.
The helmsman is prevented from saying anything to the Bellman by "Rule 42 of
the Code, `No one shall speak to the Man at the Helm,'" which the
Bellman has symmetrically amended with the words `and the man at the helm
shall speak to no one.' The "man at the helm" is, by definition, the
helmsman. But it is revealed in a footnote that the office of helmsman was not
a permanent assignment. The implication is that the helmsman, when he stopped
being helmsman, would be able to speak to the Bellman. But then the helmsman
would not be the helmsman anymore, so he wouldn't be able to speak as the
helmsman. (This play with self-reference and the essence of self is another
favourite of Dodgson's; Alice spends much thought wondering whether she can
consider herself as her self, after changing so much.)
Forty-two would have remained an insignificant feature had it not been for the
"Hitchhikers" series of novels by Douglas Adams, beginning with The
Hitchhiker's Guide to the Galaxy, in which it is revealed that the planet
earth is an artificial computing device, constructed in order to find the
ultimate question of "life, the universe, and everything", the answer to which
has already been found to be forty-two. It seems likely that Adams borrowed
this particular answer from Lewis Carroll. The earth is destroyed for a petty
motivation just before the moment of output, and as a result a replacement
planet has to be constructed and the entire computation restarted. Dodgson
would have loved this idea. So would Charles Babbage, a nineteenth-century
pioneer of automatic digital computing. If only the makers of the earth had
built in a checkpointing mechanism!
Slang: The Art of Architecture
Many subcultures have their own argot, formed by the play with analogy that
the human mind seems unable to resist. Sometimes when I am discussing with my
advisor some changes I want to make to a program, he asks me what effects my
proposed alterations would have upon other facets of the system, and I respond
with, "Oh, all this is orthogonal." What I mean is that the changes I want to
make to some parameters of the system will have no effect upon some other
parameters; the two sets of parameters are independent of each other. In
linear algebra, when two vectors are completely independent of each other, that
is, when they have no shared components pointing in a common direction, they
are said to be "orthogonal". This style of generalisation of a term based upon
an analogy constructed from its semantics recalls the Principle of the
Permanence of Equivalent Forms.
A common word overheard in the halls of the high school that I attended was
"lunshin". This was part of a local dialect of what Cran, McCrum, and MacNeil
in The Story of English term "Black English". "Lunshin", as it was
used, described a person who was temporarily being foolish. My guess is that
it was derived from the idiom of the same meaning, "out to lunch". The new
word "shody" (from "shorty", as in "Hey, shorty!") was used as a masculine
personal pronoun. The dipthong "ya", a blurring of the Southern "you-all",
often took the place of "you", in the singular as well as the plural case.
Conjugation of the verb "to be" was simplified, leaving much to context and
resulting in sentences such as "Shody lunshin" (He is being foolish), "Ya be
lunshin" (You are being foolish, or, You are foolish), "Shody been smacked
upside the head" (He has been hit on the head, or, He had been hit on the
head), and "I been at the sto'" (I was [imperfect] at the store). In
pronunciation, there is a tendency to elide final consonants and consonants
directly followed by other consonants, sometimes gliding over them, sometimes
omitting them altogether. Thus "lu(n)shi(n)" (discussed above), "ai(n)' go' do
da(t)" (ain't gonna do that), and "Lo' Boa(t)" (Love Boat, a psychedelic
drug).
When I left the linguistically fertile ground of that high school and arrived
at university I was struck with a linguistic commentary on the recreational
habits and ribaldry of many contemporary college students: the plethora of
words and phrases meaning "vomit" and/or "to vomit" (Middle English, from Latin
"vomitus", the past participle of "vomere"). At most American colleges and
universities, a weekend cannot pass without seeing multitudes puke, yuke, yak,
yag, gak, splag, zool, barf, woff, rauf, ralph, boot, heave, hurl, lose it, let
'er rip, uneat, wear their lunch, have dinner for the second time, toss their
cookies, 'gurgitate, throw up, shove up, upchuck, chuck Cheerios, toss tacos,
make macaroni, paint the pavement, shout at their shoes, feed the fish, drain
the main, swab the deck, blow lunch, blow chow, blow chunks, spew chunks, blow
groceries, upset the shopping cart, clean house, worship the porcelain, pray on
the porcelain altar, pray to the porcelain prince, drive the porcelain bus,
talk to the big white telephone, talk to Huey, talk to Ralph, scream Buick, do
the yellow-belly dance, fill the gut bucket, or deliver a street pizza, in a
cascade of technicolor yawns, 3-D yawns, chunky waterfalls, pigtracts (from
"pig extract"), liquid laughs, and reverse peristalsis. In addition there are
the more polite "disgorge" (Middle French "desgorger"), the primary meaning of
which has been broadened from that of an oral discharge to any kind of mass
discharge, and the oh-so-euphemistic British "pass up". These people are
intoxicated, inebriated, drunk, tipsy, silly, happy, buzzed, tanked, loaded,
leasing liquor, bombed, blitzed, hammered, rocked, smashed, totalled,
liquidated, sloshed, gunned, whaled, wasted, plastered, polluted, pissed,
haunted, pie-eyed, tight, gone, gonzo, gonged, out-of-it, done-like-dinner,
smokin', toasted, fried, baked, sauced, fricasséed, zambezeed, zinged,
zombied, zooed, wazooed, fucked up, and shitfaced (or just plain 'faced). This
particular lexical variety is probably not what President Frank Rhodes has in
mind when he speaks of the great "diversity" of "the Cornell community". But,
there it is.
* * *
The fascination with language and meaning evidenced in many of the works
discussed in this thesis is typical of computer science. Computer science is
an outgrowth of mathematics, and its roots lie in nineteenth-century
symbol-pushing. Much of the creativity in computer science lies in finding
ways of representing information within prescribed schemes. Many computer
scientists, uncomfortable with the freedom, intractability, and continual
evolution of natural languages as eighteenth-century natural scientists were
uncomfortable with the proposal of arbitrary taxonomies and as Hamilton was
uncomfortable with the arbitrariness of the rules of abstract algebra, try to
live in a make-believe universe of static languages. Like Lily Briscoe in
To the Lighthouse, they wish to ascend to some one perfect
representation and are frustrated with their inability to find such a
representation. This type of person, grasping for a mandated system, wishing
to be imprisoned, is like the child who protests when someone drives even one
mile per hour above the speed limit or crosses the double yellow line to pass a
standing bus.
David Gries, a professor in the computer science department at Cornell
University, seems to me a more moderate case of this type of behaviour. He
latches onto lexicons and manuals of style in an attempt to reify English
usage, and once he has found what he would like to be the standard, he
suggests--vigorously--that other people consider adopting it. One of the
distinctions that he espouses is between the semantics of "which" and those of
"that". Gries, armed with supporting references, believes that, regardless of
most spoken usage, "that" should introduce an essential qualifier, as in "the
house that was built by Jack", whereas "which" should introduce an accidental
qualifier, as in "that house, which was built by Jack". Some other members of
the department also hold this view, so that when I once gave my advisor a paper
of mine to review, I found it annotated with remarks on such "errors" when he
gave it back to me. Some people, it seems, would like to be able to treat
English more like a computer language, data in a standard format to be chewed
up and spit out by some compiler program. It is true that we need common
context in language, but at the same time, the range of expression should not
be so restricted that individual styles are hampered. In my opinion, Gries
goes too far toward the extreme of standardisation. In 1989, Gries sent this
electronic message to the department:
[An associate of mine in the department] found an author that recommends the
use of "they" in the singular for "he or she". Based on that recommendation, I
looked up "they" in the Oxford English Dictionary and found the following.
they: Often used in reference to a singular noun made universal by "every",
"any", "no", etc. or applicable to one of either sex (= "he or she").
The OED cites several examples of the latter use--i.e. of a singular noun
applicable to one of either sex. Here are two of them.
From 1759: If a person is born of a gloomy temper, they cannot help it.
From 1866: Now, nobody does anything well that they cannot help doing.
Similarly, the OED says that "them" is
often used for "him or her", referring to a singular person whose sex is not stated.
From 1874: Whenever anyone was ill, she brewed them a drink.
Similarly, the OED says that "their" is
often used instead of "his or hers" when the gender is inclusive or
uncertain.
From 1845: Every human being must do something with their senses.
From: 1898: It's enough to drive anyone out of their senses.
That's enough for me. From now on I use "they" for "he or she", "them" for
"him or her", and "their" for "his or hers".[38]
This illustrates Gries's acute awareness of the system of language that he uses
to express his thoughts, a system that most people take for granted.
Language Theory
We have seen some formal systems of expression--the propositional and
predicate calculi, the list world, and Peano Arithmetic--and we have noted the
coexisting duality of expression and meaning. On one level these formal
systems are only methods of shunting symbols. And yet, when these symbols are
given interpretations, there are correspondences between their forms and
combinations and the forms and combinations of ideas that they represent. As
Lavoisier wrote, a language is as important as the ideas expressed by it. We
have studied the ideas of formal logic and described formal languages in which
these ideas can be expressed. Now we must give more attention to the theory of
languages.
We will begin with some definitions. An alphabet is a finite set of
symbols. "Symbol" here is an undefined term; anything can function as a
symbol. We can do Peano arithmetic by forming strings of `s's or by queueing
up people at a coach stop. Chess can be played using plastic pieces on a
table, actors in a field that has been squared off, characters in Through
the Looking-Glass, or even by post, with no physical board or pieces at
all. An alphabet is conventionally denoted by the Greek letter `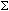 '. A
string over an alphabet is a finite sequence of symbols from the
alphabet. A symbol by itself is a string whose length is one. The
length of a string is the number of occurrences of symbols in the
string. The length of a string x is denoted by `|x|'. The
null string is the special string that contains no symbols (i.e., its
length is zero). It is represented by `
'. A
string over an alphabet is a finite sequence of symbols from the
alphabet. A symbol by itself is a string whose length is one. The
length of a string is the number of occurrences of symbols in the
string. The length of a string x is denoted by `|x|'. The
null string is the special string that contains no symbols (i.e., its
length is zero). It is represented by ` '. String variables are
usually represented by the letters u, v, w, x, y, z, and symbol
variables are usually represented by a, b, c, .... The
concatenation operation joins two strings. It is similar to
append in the lists world and to . in Peano arithmetic. Concatenation,
like multiplication in arithmetic, is symbolised either by juxtaposing two
variables and omitting the operator, as in `xy', or by the operator `.',
as in `x.y'. As nil is the identity element for append in
the lists world,
'. String variables are
usually represented by the letters u, v, w, x, y, z, and symbol
variables are usually represented by a, b, c, .... The
concatenation operation joins two strings. It is similar to
append in the lists world and to . in Peano arithmetic. Concatenation,
like multiplication in arithmetic, is symbolised either by juxtaposing two
variables and omitting the operator, as in `xy', or by the operator `.',
as in `x.y'. As nil is the identity element for append in
the lists world,  is the identity element for . in the strings
world. A substring is a string that is part of another string, that is,
string x is a substring of string y if and only if there exist
strings u and v such that y=uxv. u or v or
both may be the null string, in which cases, respectively, x is said to
be a prefix of y, a suffix of y, or simply y.
A string x superscripted with a natural number n represents
x repeated n times: a5 = aaaaa. So a
superscript n is shorthand for n-1 concatenation operations.
(n-1 concatenations, not n of them, because to repeat a string
only once does not require a concatenation; it requires only writing out the
string.) This was the origin of our meta-notation for strings of `s's in Peano
arithmetic. The superscript 0 is defined, following Peacock's Principle of the
Permanence of Equivalent Forms, as producing
is the identity element for . in the strings
world. A substring is a string that is part of another string, that is,
string x is a substring of string y if and only if there exist
strings u and v such that y=uxv. u or v or
both may be the null string, in which cases, respectively, x is said to
be a prefix of y, a suffix of y, or simply y.
A string x superscripted with a natural number n represents
x repeated n times: a5 = aaaaa. So a
superscript n is shorthand for n-1 concatenation operations.
(n-1 concatenations, not n of them, because to repeat a string
only once does not require a concatenation; it requires only writing out the
string.) This was the origin of our meta-notation for strings of `s's in Peano
arithmetic. The superscript 0 is defined, following Peacock's Principle of the
Permanence of Equivalent Forms, as producing  , the identity element
for ..
, the identity element
for ..
A language over an alphabet is a set of strings over that alphabet.
Since languages are sets, all the operations of set theory apply to languages.
Here are some of them and descriptions of what strings they generate for two
languages L0 and L1 over an alphabet 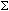 :
:
| OPERATION | GENERATES |
|---|
 | All strings over 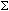 that are not in L0 that are not in L0 |
L0 L1 L1 | All strings that are in either or both of L0 and L1 |
L0 L1 L1 | All strings that are in both L0 and L1 |
The concatenation of two languages L0 and L1, denoted "L0L1", is the set of all
possible string concatenations formed by taking the first string from L0 and
the second from L1. The concatenation of a set with itself can be abbreviated
using a superscript, as the concatenation of a string with itself can be
abbreviated using a superscript. So L2 is LL,
L3 is LLL, and so on. L0 is
 . (This is not the same as the null string
. (This is not the same as the null string  ; rather, it
is the set whose only member is
; rather, it
is the set whose only member is  .) There is also the `*' operation,
called Kleene closure. (For your information, "Kleene" is pronounced
with two long `e' sounds, like "Kleenee".) Kleene closure is like
superscripting, except that the number of set product operations is a wildcard;
any string that can be produced by concatenating any number of strings in L is
in L*. So L* =
.) There is also the `*' operation,
called Kleene closure. (For your information, "Kleene" is pronounced
with two long `e' sounds, like "Kleenee".) Kleene closure is like
superscripting, except that the number of set product operations is a wildcard;
any string that can be produced by concatenating any number of strings in L is
in L*. So L* =
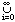 Li. For example, {a, b, c}*
= {
Li. For example, {a, b, c}*
= { , a, b, c, aa, ab, ac, ba, bb, bc, ca, cb, cc, aaa, aab, ... }
, a, b, c, aa, ab, ac, ba, bb, bc, ca, cb, cc, aaa, aab, ... }
Regular expressions are descriptions of languages. The class of languages
that can be described by regular expressions is called the regular
languages. I have never found any good reason for using the word "regular"
to describe these languages. They can be generated by rules, but so can many
languages. Perhaps the justification is that the regular languages can be
generated by very simple rules, in which case a better term than "regular"
would have been "simple". In any case, the term is entrenched. Regular
expressions are defined inductively. (L(R) is the language represented by
regular expression R.)
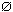 is a regular expression representing
is a regular expression representing 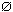 , the null set.
, the null set.
 is a regular expression representing
is a regular expression representing  , the set having
the empty string as its only member.
, the set having
the empty string as its only member.
- Any symbol a is a regular expression representing a, the set
having a as its only member.
- If r and s are regular expressions, then:
- (rs) is a regular expression representing L(r)L(s)
- (r+s) is a regular expression representing
L(r)
 L(s)
L(s)
- r* is a regular expression representing
L(r)*
Although it does not add any more expressive power to regular expressions, it
is notationally convenient to define another operation on regular expressions,
positive closure. If r is a regular expression, then r+
is a shorthand for rr*.
In other terms, L(r+) is L(r
*)- ; the resultant string must contain at
least one string from the generating set. * and
+ (positive closure) have higher precedence than ., which
has higher precedence than + (union). As usual, unneeded parentheses can be
quietly dropped. Here are some sample regular expressions and their meanings
in English:
; the resultant string must contain at
least one string from the generating set. * and
+ (positive closure) have higher precedence than ., which
has higher precedence than + (union). As usual, unneeded parentheses can be
quietly dropped. Here are some sample regular expressions and their meanings
in English:
| EXPRESSION | MEANING |
|---|
| (0+1)* | all strings of 0's and 1's |
| 0*(0+1)*1* |
all strings of 0's and 1's |
| 0*+1* |
all strings consisting only of 0's or only of 1's |
| 0*1* |
all strings over {0, 1} that do not contain the substring 10 |
| (a+b+c)+bab |
all strings of a's, b's, and c's of length at least four that have the suffix bab. |
(0+ )(10)*(1+ )(10)*(1+ ) ) |
all strings of 0's and 1's that contain neither 00 nor 11 as a substring |
| (aa)* |
all strings of a's that are of even length |
| a*b(a+b)* |
all strings of a's and b's that contain at least one b |
| (a+b)*b(a+b)* |
all strings of a's and b's that contain at least one b |
As the first two examples above demonstrate, there is more than one way to skin
a cat: Always reduce your regular expressions to simple terms that make the
effect of the expression most apparent. Also, note the difference in meaning
between (0+1)*, 0*+1*,
and 0*1*.
These forms have different effects, and beginning students often confuse them.
We have now seen four formal languages. Here is a description of similar
operations and identities in them:
| LANGUAGE | OPERATION | IDENTITY |
|---|
| propositional calculus |  | false |
|  | true |
| lists | append | nil |
| Peano arithmetic | + | 0 |
| . | s(0) |
| regular expressions | + | 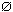 |
| . |  |
EXERCISES
0. Two regular expressions denoting the set of all strings of a's and b's that
contain at least one b are given above. There is a third simple regular
expression that denotes this set. What is it? How is it related to each of
the other two, and it what ways does it differ from each of them? Your answer
should not be in terms of the operations *, +, and .
involved in each of these regular expressions, but in terms of the different
ways in which the subexpressions in each of the regular expressions correspond
to the parts of the strings in the set that is being described.
Which of the following statements are true? Explain.
- 1. 1100
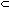 L(0*1*0*)
L(0*1*0*)
- 2. L(0*1*)
 L(1*0*)
L(1*0*) 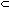 L(1*+0*)
L(1*+0*)
- 3. L(0*1*)
 L(1*0*)
L(1*0*)
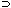 L(1*+0*)
L(1*+0*)
Describe the following regular expressions in English. Do not simply read off
the regular expression mechanically substituting English phrases for regular
expression operations. Rather, give the restriction(s) upon the strings that
are implemented by the given regular expressions. So, for example, in the
table above, the meaning of
(0+ )(10)*(1+
)(10)*(1+ )
is given not as "either a 0 or the null
string, followed by 10 any number of times, possibly followed by a 1" but as
"all strings of 0's and 1's that contain neither 00 nor 11 as a substring".
This says what the regular expression does, not how it looks.
)
is given not as "either a 0 or the null
string, followed by 10 any number of times, possibly followed by a 1" but as
"all strings of 0's and 1's that contain neither 00 nor 11 as a substring".
This says what the regular expression does, not how it looks.
- 4. a(a+b)*b
- 5. (0+10)*(1+
 )
)
- 6. (1+01+001)*(
 +0+00)
+0+00)
- 7. ((a+b)(a+b))*+((a+b)(a+b)(a+b))*
Give regular expressions for the following sets of strings over a, b:
- 8. all strings containing exactly three a's (These a's need not be adjacent.)
- 9. all strings not containing two adjacent a's
- 10. all strings not containing the substring ab
- 11. all strings containing a number of b's that is a multiple of 3
- 12. all strings in which any and all pairs of adjacent a's precede any and all pairs of adjacent b's
Languages are fundamentally connected with machines and algorithms. We shall
see that problem instances can be encoded or viewed as strings, and a problem
can be viewed as a question of deciding whether any given string is in a
particular language. This decision is more difficult for some languages than
for others, and for some it is impossible. For now let us examine the history
and theory behind some computing machines.
Babbage: The First Hacker
Charles Babbage, a co-founder of the Cambridge Analytical Society with George
Peacock and John Herschel, turned away from work in abstract algebra to devote
himself to designing and constructing automatic, mechanical computers. Babbage
was singularly devoted to this project, regularly working ten hours or more
each day. When offered the Lucasian professorship at Cambridge, the
prestiguous chair once occupied by Isaac Newton, his first impulse was to turn
down the offer because of the time that the duties of the professorship would
take away from his work. He was convinced to accept the appointment, but
eventually resigned in order to work more on his "calculating engines".
Luckily, Babbage possessed a sizable inheritance which he used to fund much of
his work. In his own time, Babbage became regarded by many as a crackpot, a
relentless peddler of impractical ideas. Babbage recognised many of the
principles of computer architechture and programming. However, the value of
his work has been noted only in retrospect, after its rediscovery, a century
later, by the mathematicians and engineers who constructed the first electronic
digital computers.
In Babbage's time many mathematical tables, such as tables of logarithms and
of astronomical constants, were calculated by human computers using the method
of differences. The method is best illustrated by example, and we choose the
same one used by Menabrea in his "Sketch of the Analytical Engine". Suppose
one wants to calculate a table of the squares. One starts off with a second
difference of 2, a first difference of 1, and the first of the
squares, 0:
0 1 2
The squares will be generated in the first column of the table. The second
column, an intermediate result, is a sequence of successive odd integers. To
derive the second row from the first, we first write down the constant second
difference, 2. Then we add the second difference of the first row, 2, to the
first difference of the first row, 1. The result, 3, is the first difference
of the second row. Finally, the first difference of the first row, 1, is added
to the first square, 0, to produce the second square, 1:
0 1 2
1 3 2
Note the pattern in which each successive row is generated from the row above
it. The new entry in the first column is the sum of the first and second
columns of the previous row. Similarly, the new entry in the second column is
the sum of the second and third columns of the previous row. Thus sums are
flowing from the rightmost column of the table, where the constant 2 is
injected at each step, to the leftmost column of the table, where the squares
are being output. The next row is (4, 5, 2). The Difference Engine, as it
existed on paper, was capable of managing seven such columns. That is, it was
restricted to the sequences whose seventh difference is 0. Note that this
calculation is based upon the simple algebraic relationship (n+1)2 = n2+(2n+1). If the rows of the
table are numbered starting from 0, then the nth row, in
general, contains the triple (n2, 2n+1, 2). If the nth row is known, then the (n+1)st row
can be easily computed. This is a simple iterative algorithm.
Babbage's childhood reveals in his personality the germ of what was to become
his life's occupation. When offered a toy some of the workings of which were
concealed, the young Babbage would demand what was inside it. If the answer
were not sufficient, the toy would be broken open, and Babbage would see for
himself. Thus the complex rules of operation of the toy would be resolved into
a synthesis of the simpler rules governing its parts. Babbage ascribes this
account of his behaviour to his mother; he himself must have been too young to
remember it. Even at that stage of his development, he felt the urge to seek
the hidden harmony. Like many other computer scientists, Babbage enjoyed
devising and foiling security systems and codes. He records an episode at
school during a period when he was sneaking out of his room at night to study
when his roommate devised alarm systems to wake him if Babbage attempted to
open the door of the room in sneaking out. In some sense Babbage's childhood
lasted his entire life. He always retained his boyhood fascinations. In his
memoirs he recounts an expedition into the crater of Vesuvius, where his native
guides refused to follow him, in which he timed the interval between small
eruptions of lava and, wanting to see a pool of molten lava, approached the
site of the eruptions during the short intervals of inactivity. What
confidence in inductive truth! Such a reckless, living Englishman!
Babbage's preoccupation with ways in which information can be conveyed led to
his later inventions. The complications of his mechanical drawings, for
example, caused him to develop a new system of mechanical notation. He later
described this as "one of the most important additions I have made to human
knowledge".[39] His computing machines, like all
computing devices, were physical encodings of arithmetical (or algebraic)
principles, as Hammurabi's Code was the embodiment of legal principles.
Babbage introduced punched cards as media for the storage of computer
instructions. The method had been used previously to control automatic looms
that wove patterns, just as the punched roll of paper in a player piano causes
the automatic reproduction of a piece of music. Ada Augusta, Countess of
Lovelace, observed with an intimate sense of the beauty of the mathematics of
the Analytical Engine, "We may say most aptly, that the Analytical Engine
weaves algebraical patterns just as the Jacquard loom weaves flowers and
leaves."[40]
It is said generally that Babbage was ahead of his time. In particular, his
ideas for automatic computing machinery were ahead of the state of technology.
The construction of Babbage's first machine, the Difference Engine, required
the prior fabrication of a collection of many new tools. It was said by some
that the 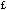 17,000 spent on the Difference Engine by the British
government was well disposed even without the completion of the project,
because of the advances in the state of the art of mechanical engineering that
accompanied the development of the Difference Engine. (This same argument is
now employed to justify spending by the Department of Defense in the United
States.) Babbage's nineteenth-century universe was still the mechanistic one
of Newton, so he never could have conceived a physical implementation of a
computing device as anything but a mechanism, an arrangement of gears, springs,
and levers. The developments in the study of electromagnetism which were to
lead to the genesis of electronics did not occur until the latter part of the
nineteenth century.
17,000 spent on the Difference Engine by the British
government was well disposed even without the completion of the project,
because of the advances in the state of the art of mechanical engineering that
accompanied the development of the Difference Engine. (This same argument is
now employed to justify spending by the Department of Defense in the United
States.) Babbage's nineteenth-century universe was still the mechanistic one
of Newton, so he never could have conceived a physical implementation of a
computing device as anything but a mechanism, an arrangement of gears, springs,
and levers. The developments in the study of electromagnetism which were to
lead to the genesis of electronics did not occur until the latter part of the
nineteenth century.
Babbage was the first hacker. He worked empirically, concerning himself more
often with getting the best performance out of a physical implementation of a
mathematical system than with specifying that system in the abstract. In this
respect he was a prime example of the English scientist, the gentleman of
independent means twiddling knobs on his apparatus and stumbling upon something
neat every once in a while. I mean "hacker" in the old sense of the word.
During the Golden Age a "hacker" was simply someone who hacked out computer
programs, using the same method, very much founded upon observation, as
Babbage. A hacker throws a program together, often introducing several bugs in
the process, and then runs it on test data in order to find and to eradicate
the bugs. A modern mathematician, in the spirit of the Continental
mathematicians of the nineteenth century, would advocate developing the program
simultaneously with a mathematical proof of its correctness. Hackers, using
the engineering approach, do not bother with such preliminaries, but jump right
into what they consider the real substance of the problem.[41] Babbage must have been aware of the significance of his
machines in terms of abstract algebraic properties, having been so active in
the Analytical Society and having written privately on the subject as early as
1821. Yet all his published writings refer to his machines in arithmetical
terms. Ada Lovelace, in her explications of Babbage's calculating engines,
refers to abstract algebra, but Babbage, as a hacker, seems to have taken the
pragmatic, real-world, arithmetical view of their functioning.
In his Ninth Bridgewater Treatise, Babbage compares the operations of
the universe to the operations of one of his calculating engines. The
Bridgewater Treatises had been the legacy of Francis Henry Egerton, Earl of
Bridgewater, who left  8000 to support the production of treatises
"on the Power, Wisdom, and Goodness of God, as manifested in the
Creation"--that is, to commission popular expository works supporting the
Argument from Design. There were eight of these Bridgewater Treatises, and
Babbage took the name "Bridgewater Treatise" for his own work, presumably to
heighten its popularity. The Ninth Bridgewater Treatise was a reply to
William Whewell, who wrote in the first of the Bridgewater Treatises that one
could not approach the divine through the "deductive", or applied, sciences.
"We have no reason whatever", wrote Whewell, "to expect from their speculations
any help, when we ascend to the first cause and supreme ruler of the
universe."[42] Babbage and Whewell had become friends at
Cambridge and were both interested in the mathematical sciences, but they had
turned in opposite directions. Babbage had given up abstract mathematics in
favour of implementing mathematics with his calculating engines, and Whewell,
possessing a broad knowledge of many scientific fields but not the insight to
make the same kinds of discoveries as his fellows, turned toward the history
and philosophy of science. How could Babbage's masses of cogs and springs,
clearly the work of humans and not a direct result of God, approach the
wonderful functioning of God's system of celestial mechanics, and his animal
and plant creatures? This was Whewell's reasoning. Babbage refrained from
blunt rebuttal of Whewell, because he agreed with the general idea that one
could approach the divine through the investigation of Nature. He wrote in his
preface:
8000 to support the production of treatises
"on the Power, Wisdom, and Goodness of God, as manifested in the
Creation"--that is, to commission popular expository works supporting the
Argument from Design. There were eight of these Bridgewater Treatises, and
Babbage took the name "Bridgewater Treatise" for his own work, presumably to
heighten its popularity. The Ninth Bridgewater Treatise was a reply to
William Whewell, who wrote in the first of the Bridgewater Treatises that one
could not approach the divine through the "deductive", or applied, sciences.
"We have no reason whatever", wrote Whewell, "to expect from their speculations
any help, when we ascend to the first cause and supreme ruler of the
universe."[42] Babbage and Whewell had become friends at
Cambridge and were both interested in the mathematical sciences, but they had
turned in opposite directions. Babbage had given up abstract mathematics in
favour of implementing mathematics with his calculating engines, and Whewell,
possessing a broad knowledge of many scientific fields but not the insight to
make the same kinds of discoveries as his fellows, turned toward the history
and philosophy of science. How could Babbage's masses of cogs and springs,
clearly the work of humans and not a direct result of God, approach the
wonderful functioning of God's system of celestial mechanics, and his animal
and plant creatures? This was Whewell's reasoning. Babbage refrained from
blunt rebuttal of Whewell, because he agreed with the general idea that one
could approach the divine through the investigation of Nature. He wrote in his
preface:
One of the chief defects of the Treatises above referred to appears to me to
arise from their not pursuing the argument to a sufficient extent. When a
multitude of apparently unconnected facts is traced up to some common
principle, we feel spontaneously an admiration for him who has explained to us
the connexion; and if, advancing another stage in the investigation, he prove
that other facts, apparently at variance with that principle, are not merely no
exceptions, but are themselves inevitable consequences of its application, our
admiration of the principle, and our respect for its discoverer, are still
further enhanced.[43]
This passage displays perhaps a tinge of egotism, concentrating as it does upon
the discoverer of a scientific principle instead of on the principle itself,
but the sentiment is clear enough. Babbage was a devotee of Laplace's idea of
a clockwork universe. Given a set of physical laws and an initial condition
for the universe, one could, if given enough time for the requisite
calculations, apply the laws iteratively and predict the state of the universe
at any particular time in the future. This spirit of determinism was "in the
air"; it was not particular to Laplace. Any reasonably intelligent child can
come up with it, and it has continued to have a great influence on modern
science. Einstein, for example, refused to accept the nondeterminism of
quantum mechanics, insisting that "God does not play dice with the universe."
Babbage took this clockwork idea and made it literal: his machines were
mechanical constructions of gears and springs, demonstrating the production of
apparently complex behaviour--the apparent harmony--by simple, mechanical,
deterministic laws--the hidden harmony.
In one chapter of his treatise, Babbage details the construction of a
clockwork machine that produces a series of numbers as its output. He
conceives of a hierarchy of levels of controlling rules. This hierarchy of
rules in Babbage's computing system is similar to the hierarchies of laws in
legal systems. In the United States, for example, the highest law is the
Constitution. It determines what other types of laws may be made, and what
precedences they are to have, and so on. Similarly, the highest rule in
Babbage's machine is the rule that determines what rule will determine the
machine's output. So, for example (after Babbage's construction), the highest
rule might say "Use rule A until the number 420 is produced. Then
switch to rule B." Rules A and B are as follows:
A Begin with the number 0, and increase by 1 on each step.
B Begin with a count of 421. On each step, produce the square of the
current value of the count and then increase the count by 1.
Babbage's construction uses a more complex set of rules, but the idea of rules
supervising other rules in the operation of a machine is the same. After
seeing the first few hundred numbers produced by the machine, any reasonable
observer would be fairly confident that the sequence being produced is a simple
succession: each number is always one greater than the previous number in the
sequence. They would have perceived the apparent harmony. But on the 421st
step, the observer would be surprised, and their world-view sent flying
topsy-turvy, by the appearance of 177,241 instead of the expected 421. Babbage
suggested such a hierarchy of controlling rules as a basis for miracles. In
this scheme, miracles were not instances of divine intervention in the
universe, but effects of higher-order rules preprogrammed into the universe
through divine foreknowledge. Obviously, the universe is more than a
collection of cogs and flywheels charged with the purpose of calculating a list
of numbers. But the analogy between the physical laws of the universe and the
computational rules of Babbage's calculating engines is a good one. And given
the basis of science in mathematics, it is not difficult to conceive of the
universe as a mathematical system. Babbage inverted Whewell's hierarchy of the
natural sciences. As the German mathematician Leopold Kronecker said in the
late nineteenth century, "God made the integers; all the rest is the work of
man."
Babbage himself is at least partly culpable for his fall into superfluity. He
was so often excited by an idea or a discovery that he plunged into work on its
implementation without enough preliminary study. As a result of the British
government's cancellation of funding for the Difference Engine, Babbage was
forced out of the domain of implementation and into one of contemplation, and
in only a few months he had come up with a much more general computing device,
the Analytical Engine. As noted above, the Difference Engine imposed a linear
flow of information, evidenced in the notation above by a right-to-left flow of
sums through the columns of differences. The Analytical Engine was described
by Babbage as the Difference Engine "eating its own tail", in an echo of
Kekulé's dream-inspiration for the structure of the benzene ring.
Information from the left could be channelled back into the machine on the
right. Such a machine was capable of all the operations of mathematical
analysis, not merely of calculating tables based upon the method of
differences. If Babbage had disciplined himself to spend more time thinking
his ideas through before beginning construction of his machines, he could have
gone to the government for funding on the Analytical Engine and followed the
design through to its implementation. As it was, Babbage would repeatedly come
up with a scheme, invest much time and money in bringing that scheme to
implementation, and then conceive a simpler scheme and abandon all the work
that had gone before. One activity upon which he wasted a great amount of
labour was the optimisation of the mechanical process of performing carries
during additions. He noted that although most of the work of addition, that of
adding the corresponding digits of the two addends, can be performed in
parallel, adding each pair of corresponding digits simultaneously, the carrying
from one place to the next was inherently sequential, because carries on the
right of a sum can induce more carries further to the left. He had many ideas
about mechanisms for anticipating the occurrence of a carry, and for storing
the carries of a running sum and adding them into the result as a final step.
He spent all his time hacking and hardly ever saw a project through to a
conclusion. Thus Babbage is another example of a scientist uncomfortable with
imperfect expression. Because he could not bring himself to accept
inefficiency when he could sense the existence of a better way of building a
machine, he flitted from one scheme to another and never stuck with his work.
His work was both a product and a victim of his compulsion to seek a perfect
representation for his ideas.
Mathematicians have constructed abstract models of computation that do away
with the complicating implementation details of real-world computers. These
types of machines are equivalent to classes of real-world computers.
"Equivalent" here means able to solve the same classes of problems. Because of
this equivalence, mathematicians can prove theorems about abstract models of
computation and know that their results apply to all real-world computers. One
wonders what Babbage, the mechanical implementor, would have thought of such
abstract machines, that exist only on paper.
A deterministic finite automaton (DFA) is a simple theoretical
computer. It is given an input string and always starts operating in a
designated initial state. Each character in the input causes the DFA to make a
state transition. The DFA can use its internal state to remember information
about the prefix of the input that it has seen so far. Together, the states
and the transitions between them are the DFA's control. The DFA
accepts the input if it is in a final state when the end of the input is
reached. Otherwise the DFA rejects the input. The DFA can pass through
a final state, when it is not at the end of the string, without accepting. A
simple example of a DFA is a combination lock. Suppose a lock requires a
4-digit combination to be entered, one digit at a time. Whenever an incorrect
digit is encountered, the lock returns to its initial configuration and the
entire combination must be re-entered from the beginning. Only when the entire
combination has been entered does the lock reach a final state and open. If
another number is entered after the correct combination, the lock resets to its
initial state. The transition diagram for one such lock with alphabet 0, 1, 2,
3, 4 looks like this.
What is the simple regular expression for the language that this DFA accepts?
Since each transition is labelled with the input symbol that causes the
transition, at any point while the DFA is operating the path that it has
followed through its control is labelled with the prefix of the input that has
been scanned so far. Formally, a DFA consists of the following five objects:
- a set of states Q
- an alphabet
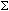
- a transition function d:QX
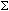 ->Q
->Q
- an initial state q0
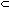 Q
Q
- a set of final states F<=Q
A DFA can also be represented in tabular form:
The only trickiness in this automaton is transitions such as the one from
SAW_0303 back to SAW_030 on symbol 0. 03030 is not a substring of the
combination, but its suffix 030 is. So it is possible that although the prefix
03 was garbage, the suffix 030 will be followed by 34 and will complete the
combination. If the transition were to return the automaton to its initial
state, such a case would be handled incorrectly. The rule being followed here
is that when a new symbol is seen in a state that is labelled with a string,
concatenate this latest symbol onto the right-hand end of the label and move to
the state labelled with the longest prefix of the resulting string. Instead of
having the lock reset when an erroneous combination is entered one may wish to
have the lock enter a state in which it refuses to accept any more input. This
can be accomplished by adding a dead state and having the automaton move
into it whenever an incorrect symbol is encountered. A dead state is a
nonfinal state whose outgoing transitions all point back to itself. Thus, if
an automaton enters a dead state, it can never move out of the dead state, so
it will never accept the input that it is reading. Since the formal definition
of a DFA requires that d be defined for every combination of state and symbol,
transitions to a dead state should exist at all points at which the automaton
determines that it definitely will not accept its input.
Constructing an automaton is one way of specifying an algorithm. The state of
an automaton is analogous to the state of the algorithm--the values of all its
variables, including the program counter, a special variable that points to the
next instruction to be executed. States should be labelled with the
information that they represent, as in the diagram above. The transition
function maps pairs of a state and a symbol to new states. It is a functional
representation of the transition arrows in the diagram above.
A DFA is finite because it can remember only a bounded amount of information.
This is because the DFA's only mechanism for memory is its state. Since the
DFA has to make a state transition for each symbol in its input, and since the
maximum-length noncircular chain of transitions among n states is of
length n-1, if the length of the input string is greater than or equal
to the number of states in the DFA then it must be the case that the DFA has
traversed at least one cycle among its states and has therefore lost some of
the information conveyed by the input. To answer a specific question about an
input, such as "Does this string have a suffix that matches the combination?",
not all the information in the string must be preserved. The question is
deciding what information to throw away.
A DFA is deterministic because there is exactly one next state when the DFA
sees a particular symbol in a particular state. The machine has no choice of
states to enter. When it sees a symbol a in a state q, it must
go to state  (q, a). Thus a deterministic machine will always traverse
the same path through its set of states when confronted with the same input.
(A nondeterministic machine has a choice of states to enter when it sees a
particular symbol in a particular state.)
(q, a). Thus a deterministic machine will always traverse
the same path through its set of states when confronted with the same input.
(A nondeterministic machine has a choice of states to enter when it sees a
particular symbol in a particular state.)
Finite automata have applications in the sense that many programs are concrete
implementations of the abstract concept of a finite automaton. However, in
most cases the link between the two concepts is obscured by differences in
structure between the program and the automaton. There are some applications,
though, in which the design of a program has been based upon the concept of a
finite automaton. Many text editors use variants of regular expressions to
specify patterns when searching for strings within a piece of text, and the
search is accomplished by constructing a finite automaton that recognises the
specified pattern. Lexical scanning, the first phase of compilation, uses a
finite automaton to recognise reserved words, numbers, identifiers, and other
categories of strings within text that is being compiled.
EXERCISES
Construct deterministic finite automata that accept the following sets of
strings:
- 0. all strings over a, b described by the regular expression (a+b)*aa
- 1. all strings over a, b containing the substring aaa
- 2. all strings over a, b not containing the substring aaa (Think: Given a
finite automaton that accepts some language L, it is very simple to turn it
into one that accepts
 . Saying that a finite automaton
accepts
. Saying that a finite automaton
accepts  is just another way of saying that it rejects
L. What part of the structure of a finite automaton causes it to accept or to
reject?)
is just another way of saying that it rejects
L. What part of the structure of a finite automaton causes it to accept or to
reject?)
- 3. all strings over 0, 1 described by the regular expression 110+(0+10)*0*1
- 4. all strings over 0, 1 that, when interpreted as binary (base 2)
representations of numbers, represent multiples of 5.
Describe (in plain English!) the languages accepted by these automata:
* * *
The nondeterministic finite automaton (NFA) is a generalisation of the
deterministic finite automaton. Nondeterminism is a relaxation of constraints.
A simple nondeterministic algorithm is the problem of finding all the items on
a shopping list inside a supermarket. The items are located at various points
along various aisles, and each of these locations must be visited. A path
containing all these points must be constructed. But there are many possible
paths, and the choice of one particular path is left to the shopper.
Similarly, an NFA has a choice of transitions out of any particular state on
any particular symbol. The formal definition of an NFA is the same as that of
a DFA except that the transition function maps to 2Q, not
to Q. The set 2Q is called the power set
of Q. Its elements are the subsets of Q. The power set of 0, 1,
2, for example, is 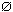 , 0, 1, 2, 0, 1, 0, 2, 1, 2, 0, 1, 2. The
notation for power sets is in the spirit of Peacock; it arises from the fact
that for any set S, |2S| = 2
, 0, 1, 2, 0, 1, 0, 2, 1, 2, 0, 1, 2. The
notation for power sets is in the spirit of Peacock; it arises from the fact
that for any set S, |2S| = 2 .
Since the transition function in an NFA maps into the
power set of the set of states, the result is a set of states instead of a
single state. From this set the machine chooses a next state. Because of the
nondeterminism, there may be paths labelled with the input string that end on
nonfinal states as well as ones that do end on final states. The path is
chosen in such a way that if there is any path that terminates on a final
state, it will be the path selected. If there is more than one such path
terminating on a final state, the particular choice of path does not matter.
.
Since the transition function in an NFA maps into the
power set of the set of states, the result is a set of states instead of a
single state. From this set the machine chooses a next state. Because of the
nondeterminism, there may be paths labelled with the input string that end on
nonfinal states as well as ones that do end on final states. The path is
chosen in such a way that if there is any path that terminates on a final
state, it will be the path selected. If there is more than one such path
terminating on a final state, the particular choice of path does not matter.
One way of looking at this is that the NFA magically guesses the correct path,
if one exists, and chooses its next state accordingly. When one is solving a
maze in a puzzle book, the problem is made easier by one's ability to see the
whole maze at once: it is all laid out on the page. But if a real copy of such
a maze were made and a person were placed into it, the problem would be more
difficult. The person would not be able to refer to the complete structure of
the maze in deciding which way to turn at a branch in a passageway. They would
have to choose blindly and explore. If they explored all of the maze, then
they could produce a map that would allow them to perform the "magic" of making
the correct choice at all branching points.
Another view is that whenever there is a choice to be made the NFA makes one
copy of itself for each possible choice and makes a different choice in each
copy. Going back to the case of the maze explorer, suppose they have the
ability to duplicate themselves. At each branch, they can continue in one
direction and send a duplicate in every other direction. Then the duplicates
can duplicate themselves when they arrive at branch points, and so on. When
the explorer (or any of their duplicates) comes to a dead end, they die. In
this way, it is guaranteed that some copy of the explorer will find a way out
of the maze, if one exists. This is similar to the "many-worlds" philosophy of
quantum mechanics, in which every time there is a nondeterministic choice to be
made, new copies of the universe arise in which the outcome is different. The
advantages of NFA's over DFA's are that they usually have fewer states and that
they are often easier to construct and to understand. They do have the
disadvantage of being more difficult to simulate on a deterministic computer.
You may remember a regular expressions exercise in which you were given two
simple regular expressions denoting the set of all strings over a, b containing
at least 1 `b' and were asked to find a third simple regular expression
denoting this set. The three expressions are a*b(a+b)*,
(a+b)*ba*,
and (a+b)*b(a+b)*. The middle term
in each of these expressions is `b'. The expressions differ in terms of which
`b' in each accepted string is denoted by the middle `b' term. The `b' term in
the first expression must correspond to the first `b' in the string, since the
first term in this expression generates only strings of `a's. Similarly, the
`b' term in the second expression must correspond to the last `b' in the
string. The third expression is more interesting. Its middle term can
correspond to any `b' in the string. This correspondence is nondeterministic;
there is a choice involved. Here is an NFA whose construction follows the form
of this regular expression.
Of the two other expressions, one corresponds to a DFA and the other
corresponds to an NFA. Which is which? Try to construct these two automata.
It may seem that both expressions must correspond to deterministic machines,
since the `b' term in each of them corresponds to a specific `b' in each
accepted string. But remember that a regular expression can be read from right
to left as well as from left to right, whereas a finite automaton always works
on its input from left to right.
Does the addition of nondeterminism add any computing power to finite
automata? What we mean by "power" in this context is not the ability to do
computations faster, but the ability to do computations at all. Are there any
problems that can be solved, in any amount of time, by an NFA but cannot be
solved by a DFA? The answer is no. This can be proven by showing, for any
given NFA, how to construct a DFA to simulate it. This process is called the
subset construction. We have seen that the names of the states of an
automaton are arbitrary and that the states can have labels that suggest the
information that they represent. Just as we can label a state "I have just
seen the suffix 030" or "I have seen a `b'", we can label the states in this
new DFA "The NFA that I am simulating would currently be in one of the
following states: ...". So whenever the NFA is in some state q, the DFA
is in a state whose label contains the name `q'. The trick here is
noticing the correspondence between states and names of states.
Obviously we cannot pack more than one state of the original NFA into a single
state of the new DFA. But we can pack the names of several states in
the NFA into the name of a single state in the DFA. We construct a DFA
whose states are labelled with subsets of the names of the states of the
original NFA. Suppose the NFA has states Q, alphabet 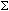 ,
transition function
,
transition function  , initial state q0, and final states F.
Then the resultant DFA has states Q', the same alphabet
, initial state q0, and final states F.
Then the resultant DFA has states Q', the same alphabet 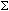 ,
transition function
,
transition function  ', initial state q0', and final states
F', defined interms of the original (Q,
', initial state q0', and final states
F', defined interms of the original (Q, 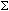 ,
,
 , q0,
F) as follows:
, q0,
F) as follows:
- Q' = 2Q Most likely not all the members of the
power set will need to be included, but there is nothing that says that there
can be no unreferenced states.
- q0' = [q0] The only state that the NFA can be in when it
starts is, by definiton, its initial state.
- For each symbol a
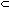
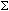 , d'([q1,
q2, ..., qm], a) is a state whose label is the union of
the names of all the NFA states that can be reached from at least one of the
qi by a transition on a.
, d'([q1,
q2, ..., qm], a) is a state whose label is the union of
the names of all the NFA states that can be reached from at least one of the
qi by a transition on a.
- F' is all states in Q' whose labels contain the name of at
least one final state of the NFA. Remember, if there is any path that leads to
a final state at the end of the input, the NFA will choose such a path.
Therefore it is sufficient to have the name of only one final state in the
label of a state of the new machine in order to make it a final state of the
new machine.
An example will illustrate the construction. Here is an NFA that accepts the
language of the regular expression (0+1)*00.
We wish to transform this NFA into a DFA. The start state of the new machine
will be [INIT].  (INIT, 0) in the NFA is the set of states INIT, ZERO_1, so
(INIT, 0) in the NFA is the set of states INIT, ZERO_1, so
 '([INIT], 0) in the DFA must be the single state labelled [INIT,
ZERO_1].
'([INIT], 0) in the DFA must be the single state labelled [INIT,
ZERO_1].  (INIT, 1) is INIT, so
(INIT, 1) is INIT, so  '([INIT], 1) must be [INIT]. Now we
have referenced another new state in the DFA, so we need to compute its
outgoing transitions. A good way to keep track of the work that still has to
be done is to make a list of all the new states that are referenced. When you
begin, the list should contain the single state q0', the initial state
of the new machine. Each time a previously unreferenced state is referenced,
add it to the list. Work in a loop, taking states off the list and computing
their outgoing transitions. Since the new states are all members of the power
set of the set of old states, the most there can be of them is
2
'([INIT], 1) must be [INIT]. Now we
have referenced another new state in the DFA, so we need to compute its
outgoing transitions. A good way to keep track of the work that still has to
be done is to make a list of all the new states that are referenced. When you
begin, the list should contain the single state q0', the initial state
of the new machine. Each time a previously unreferenced state is referenced,
add it to the list. Work in a loop, taking states off the list and computing
their outgoing transitions. Since the new states are all members of the power
set of the set of old states, the most there can be of them is
2 . If you start with an eight-state NFA, that's only 256
states! (Fortunately, the actual number of states produced by the subset
construction is usually much less than this exponential upper bound.) We
continue in the construction by computing the outgoing transitions of the new
state [INIT, ZERO_1].
. If you start with an eight-state NFA, that's only 256
states! (Fortunately, the actual number of states produced by the subset
construction is usually much less than this exponential upper bound.) We
continue in the construction by computing the outgoing transitions of the new
state [INIT, ZERO_1].  (ZERO_1, 0) = ZERO_2, and we have already seen that
(ZERO_1, 0) = ZERO_2, and we have already seen that
 (INIT, 0) = INIT, ZERO_1. So d'([INIT, ZERO_1], 0) is the state
labelled with ZERO_2
(INIT, 0) = INIT, ZERO_1. So d'([INIT, ZERO_1], 0) is the state
labelled with ZERO_2 INIT, ZERO_1, [INIT, ZERO_1, ZERO_2]. The final
construction is this.
INIT, ZERO_1, [INIT, ZERO_1, ZERO_2]. The final
construction is this.
Another extension to finite automata is the allowance of  -moves.
An
-moves.
An  -move is a transition that consumes no symbol. Since
concatenating
-move is a transition that consumes no symbol. Since
concatenating  to a string does not change the string, any number of
transitions labelled
to a string does not change the string, any number of
transitions labelled  may occur in a path without affecting the
string of symbols that labels it. The formal definition of an NFA with
may occur in a path without affecting the
string of symbols that labels it. The formal definition of an NFA with
 -moves is the same as that for an NFA without
-moves is the same as that for an NFA without  -moves
except that d maps from QX(
-moves
except that d maps from QX(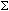

 ) instead of
from QX
) instead of
from QX . This minor alteration in the formal definition is
what allows transitions to be labelled with
. This minor alteration in the formal definition is
what allows transitions to be labelled with  .
.  -moves
make it easier to build automata from regular expressions. It is easy to
define recursively a way to build up an NFA with
-moves
make it easier to build automata from regular expressions. It is easy to
define recursively a way to build up an NFA with  -moves that accepts
exactly the language of a given regular expression. This process is described
in the figure.
-moves that accepts
exactly the language of a given regular expression. This process is described
in the figure.
The subset construction works on NFA's with  -moves with two slight
modifications. These modifications make use of the operation
-moves with two slight
modifications. These modifications make use of the operation
 -CLOSURE. For a state q,
-CLOSURE. For a state q,
 -CLOSURE(q) is the set of all states that are reachable
from q by traversal of a path labelled
-CLOSURE(q) is the set of all states that are reachable
from q by traversal of a path labelled  . This path may
consist of zero, one, or more transitions. Thus q is always an element
of
. This path may
consist of zero, one, or more transitions. Thus q is always an element
of  -CLOSURE(q). In the subset construction on an NFA with
-CLOSURE(q). In the subset construction on an NFA with
 -moves the new initial state is the state whose label is the names
of the sets in the
-moves the new initial state is the state whose label is the names
of the sets in the  -CLOSURE of the old initial state. So if the old
initial state q0 has
-CLOSURE of the old initial state. So if the old
initial state q0 has  -moves to q1 and to q2,
then the new initial state is [q0, q1, q2]. Instead of
the union of all the next states of each state in the label, the new next state
is the union of the
-moves to q1 and to q2,
then the new initial state is [q0, q1, q2]. Instead of
the union of all the next states of each state in the label, the new next state
is the union of the  -CLOSUREs of all these next states.
-CLOSUREs of all these next states.
You have seen that DFA's, NFA's without  -moves, and NFA's with
-moves, and NFA's with
 -moves are all equivalent. You have also seen that there is an NFA
with
-moves are all equivalent. You have also seen that there is an NFA
with  -moves (and therefore an NFA without
-moves (and therefore an NFA without  -moves and a
DFA) for any regular expression. This raises the question of whether or not
finite automata and regular expressions are equivalent in power, of whether or
not there is a regular expression for any finite automaton. We prove that this
is so by showing how to construct a regular expression whose language is the
same as that of a given DFA.
-moves and a
DFA) for any regular expression. This raises the question of whether or not
finite automata and regular expressions are equivalent in power, of whether or
not there is a regular expression for any finite automaton. We prove that this
is so by showing how to construct a regular expression whose language is the
same as that of a given DFA.
Number the states of the DFA from 1 to n, and let q1 be the
initial state. Let R[kij] denote the set of strings
that take the DFA from state qi to state qj without passing
through any state numbered higher than k. To "pass through" a state is
to enter it and then leave it; therefore the path may begin and/or end on a
state numbered higher than k without passing through any state numbered
higher than k. Since there are only n states in the machine,
R[nij]denotes all the strings that label paths from
qi to qj. R[kij] for any (i, j, k)
can be defined recursively. Any string that takes the DFA from state
qi to state qj without passing through any state numbered higher
than k falls into one of two cases. It may take the machine from
qi to qj without passing through k. In this case, the
string is in R[k-1 i j]. Or it may cause the machine
to pass through k one or more times. Such a string can be analysed into
several parts. The first part will take the machine from qi to
qk without passing through qk or any other state numbered higher
than k-1. This substring is in R[k-1 i k].
The second part can continue through qk and then loop back to qk
zero or more times. On each circuit from qk back to qk, the
machine will not pass through qk; it will only begin and end on
qk. So this substring is in (R[k-1 k k])*.
The third part will take the machine out of
qk for the final time and continue to qj. This substring is in
R[k-1 k j]. So R[kij]can
be defined as the union of the two cases:
R[kij] = R[k-1 i j] R[k-1 i k](R[k-1 k k])*R>k-1 k j]
R[k-1 i k](R[k-1 k k])*R>k-1 k j]
The base case is R[0ij],the set of strings that
takes the automaton from state qi to state qj without passing
through any state. If qi and qj are not neighbours,
R[0ij]must be empty, because the machine would have to
pass through some intermediate state in order to get to from qi to
qj. If qi and qj are neighbours, then
R[0ij]is the set of all symbols that label transitions
from qi to qj. If i = j, then
R[0ij] contains  as well as all these symbols.
as well as all these symbols.
R[0ij] = i!=j -> a |
 (qi, a) = qj
(qi, a) = qj
[] i=j -> a |  (qi, a) =
qj
(qi, a) =
qj 

Regular expressions can be constructed easily from these sets. The regular
expression for the base case is the union of the symbols that label the
transitions from qi to qj (and also  , if
i=j). A DFA accepts a string if and only if that string takes it
from its initial state q1 to one of its final states. So the language
of a DFA is
, if
i=j). A DFA accepts a string if and only if that string takes it
from its initial state q1 to one of its final states. So the language
of a DFA is  [qj
[qj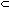 F]
R[n1j]. If r[kij] is the
regular expression whose language is the set R[kij],
then the regular expression for the language of the DFA is
r[n1 f0] + r[n1 f1] + ... +
r[n1 fm], where the fi are the final states.
F]
R[n1j]. If r[kij] is the
regular expression whose language is the set R[kij],
then the regular expression for the language of the DFA is
r[n1 f0] + r[n1 f1] + ... +
r[n1 fm], where the fi are the final states.
In the combination-lock DFA from earlier in this discussion, number INIT 1,
SAW_0 2, SAW_03 3, SAW_030 4, SAW_0303 5, and SAW_03034 6. Since the only
final state is SAW_03034, which has been assigned the number 6, a regular
expression corresponding to this automaton is r[61
6]. We can solve for this value recursively. Only a small portion of
the derivation is presented here; enduring the entire process would be nothing
but tedium. For our purposes, the process of constructing a regular expression
from a DFA is less important than the theoretical equivalence that the
existence of such a construction algorithm establishes between finite automata
and regular expressions. Here, then, is a short, representative example. Do
not bother to peruse it in its entirety; it is too tedious to be of much value
other than as a reference.
r[12 2] = r[02 1](r[01 1])*r[01 2]
= (0+1+2+4)( +1+2+3+4)*0
+1+2+3+4)*0
= (0+1+2+4)(1+2+3+4)*0
r[12 3] = r[02 3] +
r[02 1](r[01
1])*r[01 3]
= 3 + r[02 1](r[01
1])*
= 3
r[13 3] = r[03 3] +
r[03 1](r[11 1])*r[01 3]
=  + r[03 1](r[11
1])*
+ r[03 1](r[11
1])*
= 
r[13 4] = r[03 4] +
r[03 1](r[01 1])*r[01 4]
= 0 +  (r[01 1])*r[01
4]
(r[01 1])*r[01
4]
= 0
r[14 2] = r[04 2] +
r[04 1](r[01 1])*r[01 2]
=  + (0+1+2+4)(
+ (0+1+2+4)( +1+2+3+4)*0
+1+2+3+4)*0
= (0+1+2+4)(1+2+3+4)*0
r[14 4] = r[04 4] +
r[04 1](r[01 1]
)*r[01 4]
=  +
+  (r[01 1])*r[01 4]
(r[01 1])*r[01 4]
= 
r[23 3] = r[13 3] +
r[13 2](r[12 2])*r[12 3]
=  +
+  (r[12 2])*r[12 3]
(r[12 2])*r[12 3]
= 
r[23 4] = r[13 4] + r[13
2](r[12 2])*r[12 4]
= 0 +  (r[12
2])*r[12 4]
(r[12
2])*r[12 4]
= 0
r[24 3] = r[14 3] + r[14
2](r[12 2])*r[12 3]
=  + (0+1+2+4)(1+2+3+4)*0((0+1+2+4)(1+2+3+4)*0)*3
+ (0+1+2+4)(1+2+3+4)*0((0+1+2+4)(1+2+3+4)*0)*3
= (0+1+2+4)(1+2+3+4)*0((0+1+2+4)(1+2+3+4)*0)*3
r[24 4] = r[14 4] +
r[14 2](r[12 2])*r[12 4]
=  + r[14 2](r[12
2])*
+ r[14 2](r[12
2])*
= 
r[34 4] = r[24 4] +
r[24 3](r[23 3])*r[23 4]
=  + (0+1+2+4)(1+2+3+4)*0((0+1+2+4)(1+2+3+4)*0)*3
+ (0+1+2+4)(1+2+3+4)*0((0+1+2+4)(1+2+3+4)*0)*3 *0
*0
=  + (0+1+2+4)(1+2+3+4)*0((0+1+2+4)(1+2+3+4)*0)*30
+ (0+1+2+4)(1+2+3+4)*0((0+1+2+4)(1+2+3+4)*0)*30
You can see why this process is almost never done by hand! It is easy to write
a program to implement the algorithm, though.
This completes a demonstration of the equivalence of all three types of
automata that we have seen and regular expressions. Here is a diagram of the
reductions that we have shown between them. The arrows are labelled with the
name of the proof that was used. They can be read as "can be simulated by".
By now you have noticed that there is more than one finite automaton that can
accept any given regular language. Some automata are needlessly complex Rube
Goldberg contraptions, with spaghetti-like transition diagrams. Is there any
sure-fire way of finding the simplest automaton that will solve a given
problem? And how is the hand-waving nebulosity of "simplest" made formal? It
is reasonable to define "simplest" as "having the fewest possible states". An
algorithm for finding a minimum-state DFA equivalent to any given DFA will be
given. When combined with the algorithms already presented for conversions
between regular expressions and various types of finite automata, this forms a
method of finding the minimum-state DFA accepting any regular language
specified in any of these formalisms.
An extended definition of the d function of a DFA will simplify the statement
of the algorithm. We will extend d so that it takes a string as a parameter
rather than only a single symbol. For any state q in the DFA's control
and any string x over 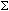 ,
,  `(q, x) will yield the state
reached by the DFA after traversing the path labelled x that begins at
q. In the three cases of the definition that follows, a is any
symbol in the alphabet of the DFA, and x is any string over the alphabet
of the DFA.
`(q, x) will yield the state
reached by the DFA after traversing the path labelled x that begins at
q. In the three cases of the definition that follows, a is any
symbol in the alphabet of the DFA, and x is any string over the alphabet
of the DFA.
 `(q,
`(q,  ) = q
) = q
 `(q, a) =
`(q, a) =  (q, a)
(q, a)
 `(q, xa) =
`(q, xa) =  (
( `(q, x), a)
`(q, x), a)
A string x is a witness for a pair of states qi,
qj if and only if one of  `(qi, x) and
`(qi, x) and  `(qj,
x) is a final state and the other is not. It follows that
`(qj,
x) is a final state and the other is not. It follows that  is a witness for a pair consisting of a final state and a nonfinal state, and
only for such pairs. Why does one use the term "witness"? Such a string bears
witness to the fact that the two states do not always effect the same actions
when given the same strings as inputs. Somewhere down the line, perhaps after
many transitions, the machine can end up in a final state in one case but not
in the other. This means that these two states are inherently distinct, that
they must be separate in order to preserve the information that the DFA needs
in order to decide whether or not some string is in its language. States in
groups that have no witnesses to distinguish them from each other are
equivalent. The members of each of these groups can be merged into a
single state.
is a witness for a pair consisting of a final state and a nonfinal state, and
only for such pairs. Why does one use the term "witness"? Such a string bears
witness to the fact that the two states do not always effect the same actions
when given the same strings as inputs. Somewhere down the line, perhaps after
many transitions, the machine can end up in a final state in one case but not
in the other. This means that these two states are inherently distinct, that
they must be separate in order to preserve the information that the DFA needs
in order to decide whether or not some string is in its language. States in
groups that have no witnesses to distinguish them from each other are
equivalent. The members of each of these groups can be merged into a
single state.
To find out which states, if any, are redundant, we can work backwards from
the final states. We set up a triangular-shaped table that has one entry for
every possible unordered pair of states. We begin by marking all pairs of a
final state and a nonfinal state as non-equivalent. This is the base case.
Now we loop through the table marking pairs that have witnesses, until we reach
an iteration during which no marks are added. On each run through the table,
for each pair of states (qi, qj) that is not already marked as
having a witness, we examine  (qi, a) and
(qi, a) and  (qj, a)
for every symbol a in the alphabet. If for some a the pair of
states (
(qj, a)
for every symbol a in the alphabet. If for some a the pair of
states ( (qi, a),
(qi, a),  (qj, a)) is marked as having a
witness, then we mark (qi, qj) as having a witness. For if some
string x is a witness for (
(qj, a)) is marked as having a
witness, then we mark (qi, qj) as having a witness. For if some
string x is a witness for ( (qi, a),
(qi, a),  (qj,
a)), then ax is a witness for (qi, qj). In this
way we make progress backwards along the transitions, beginning at the final
states and continuing until we have covered the entire machine. Once this
process is complete, we can construct a new DFA in which any and all groups of
equivalent states have been merged into single states.
(qj,
a)), then ax is a witness for (qi, qj). In this
way we make progress backwards along the transitions, beginning at the final
states and continuing until we have covered the entire machine. Once this
process is complete, we can construct a new DFA in which any and all groups of
equivalent states have been merged into single states.
For example, suppose that we want to minimise this DFA.
For convenience in illustrating the operation of the algorithm, we will mark
entries in the table with the number of the iteration on which the two states
were found to have a witness. We begin, then, by marking a 0 in all the spaces
corresponding to a nonfinal state and a final state. Now, on the first
iteration of the algorithm, we examine every space in the table that is still
blank, trying to establish witnesses. The first pair that we look at on this
iteration is (C, A).  (C, 0) = D and
(C, 0) = D and  (A, 0) = B. We go to the space in the
table that corresponds to the pair (D, B) and see that this space has not yet
been marked. Since we don't yet know that D and B are distinct, we can't use
the 0 transition to distinguish C and A. Now we try the 1 transition. The
situation here is more productive. On a 1, C goes to E and A goes to G.
States E and G have been marked as distinct, so we now mark the space for the
pair (C, A). Note that what we have just done is computed a witness for (C,
A), namely, the string 1. (Remember that
(A, 0) = B. We go to the space in the
table that corresponds to the pair (D, B) and see that this space has not yet
been marked. Since we don't yet know that D and B are distinct, we can't use
the 0 transition to distinguish C and A. Now we try the 1 transition. The
situation here is more productive. On a 1, C goes to E and A goes to G.
States E and G have been marked as distinct, so we now mark the space for the
pair (C, A). Note that what we have just done is computed a witness for (C,
A), namely, the string 1. (Remember that  is a witness for (E, G),
since E is a final state and G is not.) We continue in this manner, and at the
end of our first pass through the table, the only pairs that have not yet been
marked are (B, A), (D, A), (G, A), (D, B), (G, B), (F, C), and (G, D). During
this first pass through the table, we have been unable to distinguish these
pairs of states using either their 0 transitions or their 1 transitions.
However, we did distinguish some pairs during this pass, and this new
information may allow us to make more distinctions in our next pass. On the
second iteration, we mark (B, A), (D, B), (G, B), (F, C), and (G, D). On the
third, we mark (G, A). Going into the fourth iteration, the only unmarked
space is (D, A). But states D and A both have the same outgoing transitions.
Therefore, there is no way to distinguish them. Since no more spaces in the
table can be marked, the algorithm terminates. The minimised DFA has states D
and A merged.
Here is how the table looks at the end of the algorithm:
is a witness for (E, G),
since E is a final state and G is not.) We continue in this manner, and at the
end of our first pass through the table, the only pairs that have not yet been
marked are (B, A), (D, A), (G, A), (D, B), (G, B), (F, C), and (G, D). During
this first pass through the table, we have been unable to distinguish these
pairs of states using either their 0 transitions or their 1 transitions.
However, we did distinguish some pairs during this pass, and this new
information may allow us to make more distinctions in our next pass. On the
second iteration, we mark (B, A), (D, B), (G, B), (F, C), and (G, D). On the
third, we mark (G, A). Going into the fourth iteration, the only unmarked
space is (D, A). But states D and A both have the same outgoing transitions.
Therefore, there is no way to distinguish them. Since no more spaces in the
table can be marked, the algorithm terminates. The minimised DFA has states D
and A merged.
Here is how the table looks at the end of the algorithm:
B 2
C 1 1
D 2 1
E 0 0 0 0
F 1 1 2 1 0
G 3 2 1 2 0 1
A B C D E F
MORE EXERCISES
- 8. Construct an NFA that accepts all strings over a, b such that some
two a's are separated by a string whose length is a multiple of 4. (Note that
0 is a multiple of 4.)
- 9. Construct an NFA that accepts all strings over 0, 1 in which the eighth
symbol from the right exists (i.e., the string is at least eight symbols long)
and is a 1.
- 10. Construct a DFA equivalent to the following NFA:
- 11. Minimise the DFA that you constructed in exercise 10.
- 12. Write a program that implements the subset construction. The program must
receive an NFA or NFA with
 -moves as input and generate an
equivalent DFA as output. Input and output can be in any format that you find
convenient. Give some forethought to what data structures you'll use to
represent the automata inside the program. See also exercise 13.
-moves as input and generate an
equivalent DFA as output. Input and output can be in any format that you find
convenient. Give some forethought to what data structures you'll use to
represent the automata inside the program. See also exercise 13.
- 13. Write a program that implements the DFA minimisation algorithm given above.
(Extra karma: connect this program to the one that you wrote for exercise 12,
so that you have a program that computes the minimal DFA equivalent to any
given NFA.)
Turing and an Abstract Model of Computation
A century after Babbage, Alan Turing, with the backing of electronics, was
instrumental in bringing the automatic computer to realisation. Like Babbage,
Turing interested himself in the mathematical theory of computation and in the
practical engineering needed to implement mathematics in a physical computer.
In Turing, this engineering interest took the form of electronics. Had Babbage
lived a century later than he did, he would have concerned himself with
electrical engineering instead of mechanical engineering. Whereas Babbage's
encoding of mathematics was mechanical, Turing's was electrical. Turing did
experiment with a special-purpose mechanical computer designed to calculate
zeroes of the zeta-function, a function describing the thinning out of the
prime numbers. In another echo of Babbage, Turing never completed construction
of the zeta-function machine, although his progress was interrupted by World
War II instead of by a funding cut.
Just before the war Turing published a paper entitled "On Computable Numbers,
with an Application to the Entsceidungsproblem". The
Entscheidungsproblem, proposed by Hilbert, was the question of whether
or not there was a mathematical procedure for ascertaining the decidability
of any mathematical problem. That is, given some mathematical assertion,
is there a way to decide whether or not that assertion is provable? Gödel
had already proven the existence, within all mathematical systems of sufficient
expressive power, of statements that are true but unprovable within the system.
Thus the Entscheidungsproblem had great importance: if there were always
a procedure for ascertaining whether or not an assertion were provable, then
the unprovable statements of Gödel could be detected and pruned from
mathematics, excluded from mathematical enquiry. In "On Computable Numbers"
Turing showed that in the general case these statements could not be detected.
The mathematical model of computation advanced by Turing in "On Computable
Numbers", which became known as the "Turing Machine", has been a fundamental
abstraction in the theory of computation. A Turing Machine consists of a
finite control, corresponding to the program in a modern electronic computer or
the sequences of punched cards that were to be fed into the Analytical Engine,
and a semi-infinite tape, corresponding to a computer memory. The finite
control is like a finite automaton. It can remember information by itself, but
only a finite amount of information. The tape is the big difference between a
Turing Machine and a finite automaton. Since the tape is semi-infinite (it has
a left end, but is unbounded on the right), it can be used to store an
unbounded amount of information. The tape is divided into cells. On each tape
cell a symbol from an alphabet can be written. Remember that we think of
"alphabet" in the abstract sense here, as an arbitrary collection of symbols.
If we view each byte in the memory of an electronic computer as one cell, then
the alphabet of the computer can be viewed as the integers from 0 to 255
inclusive (255=28-1). The only restriction upon it is
that the number of symbols must be finite. The control, the program, is a
collection of rules that describe the behaviour of the Turing Machine in any
state. You can see why the control is restricted to being finite; an
infinitely long program could not be specified explicitly. (Even if you spent
all your life on it, you would make no progress in writing an infinitely long
program. This would be a hacker's nightmare.) The control is always in one of
a finite number of states, just as in a finite automaton. At any time during
the operation of the Turing Machine, its configuration is fully described by
the state of the finite control, the contents of the tape, and the position of
the read/write head. Similarly, in an electronic stored-program computer, the
configuration is fully described by the location of the instruction within the
program that is about to be executed and the contents of the memory.
Confronted with a symbol under the read/write head while in some state, the
finite control replaces that symbol with another symbol (possibly the same
symbol) and either moves the head left one cell, moves the head right one cell,
or halts. Then the control enters a new state (unless the machine has halted).
This simple construction of finite control and memory, reminiscent of the
Analytical Engine, can compute any function that can be computed. Because of
this equivalence of the Turing Machine to all other general-purpose computers,
computer scientists can prove theorems about the simple Turing Machine and be
assured that those theorems apply to all the complexities of real-world
computing devices. Finite automata can be viewed as a special case of Turing
Machines in which the control is restricted from writing on the tape and from
moving the read/write head left.
Formally, a Turing Machine consists of seven objects (Q,  ,
,
 ,
,  , q0, B, F):
, q0, B, F):
- Q is a finite set of states.
 is a finite input alphabet.
is a finite input alphabet.
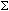 is a finite tape alphabet.
is a finite tape alphabet.
 :Qx
:Qx ->Qx
->Qx xleft, right is a transition
function that tells the machine what new state to enter, what symbol to write
onto the tape, and which direction to move the read/write head when the finite
control is in a given state and the read/write head is scanning a given
symbol.
xleft, right is a transition
function that tells the machine what new state to enter, what symbol to write
onto the tape, and which direction to move the read/write head when the finite
control is in a given state and the read/write head is scanning a given
symbol.
- q0 is the initial state.
- B
 is the blank symbol.
is the blank symbol.
- F is the set of final states.
 need not be defined for all possible pairs of a state and a tape symbol. In
cases in which d is undefined, the machine halts. If it is in a final state
when this occurs, it accepts. Otherwise, it rejects. Sometimes it does not
matter whether the machine accepts its input or not, for for some problems the
output is not in the form of an acceptance or rejection decision, but in the
form of an output string left on the tape when the machine halts. The input
alphabet is as in a finite automaton. But in a Turing Machine there is also a
tape alphabet that contains the symbols that the Turing Machine can write onto
its tape. This tape alphbet,
need not be defined for all possible pairs of a state and a tape symbol. In
cases in which d is undefined, the machine halts. If it is in a final state
when this occurs, it accepts. Otherwise, it rejects. Sometimes it does not
matter whether the machine accepts its input or not, for for some problems the
output is not in the form of an acceptance or rejection decision, but in the
form of an output string left on the tape when the machine halts. The input
alphabet is as in a finite automaton. But in a Turing Machine there is also a
tape alphabet that contains the symbols that the Turing Machine can write onto
its tape. This tape alphbet, 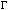 , must contain at least one symbol that
is not in
, must contain at least one symbol that
is not in 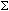 . This symbol is the blank. When the Turing Machine begins
running, the leftmost portion of its tape contains the input string, and the
tape is padded on the right with an infinity of blanks. You can see why this
special blank symbol is needed. If the input string were allowed to contain
blanks, it would be impossible for the Turing Machine to find the end of the
input. It could scan outward on its tape and find a million blanks, and it
would still not be sure whether it had passed the end of its input, because
there would still be the possibility that the next character might be
non-blank.
. This symbol is the blank. When the Turing Machine begins
running, the leftmost portion of its tape contains the input string, and the
tape is padded on the right with an infinity of blanks. You can see why this
special blank symbol is needed. If the input string were allowed to contain
blanks, it would be impossible for the Turing Machine to find the end of the
input. It could scan outward on its tape and find a million blanks, and it
would still not be sure whether it had passed the end of its input, because
there would still be the possibility that the next character might be
non-blank.
A simple language that can be accepted by a Turing Machine and not by any
finite automaton is {0n1n | n>=0}.
(This differs from 0*1*,
which can be accepted by a finite
automaton. 0n1n is a subset of
0*1* in which the number of 0's must
equal the number of 1's.) If this is not obvious to you immediately, try to
construct a finite automaton that accepts it. What barrier do you run up
against? A finite automaton cannot count indefinitely. Sooner or later it
reaches the limit of its storage capacity, whatever that capacity is. The only
way that a finite automaton can remember a piece of information is by changing
its state, and there can be only finitely many states. For any finite
automaton, the language {0n1n | n>=0}
contains an infinity of instances that are
beyond the storage capacity. Another interesting and simple example is the
question of deciding whether a given number is prime. (The number can be given
in any base. The simplest case to deal with is that of a unary number, in
which any number n is represented by a string of 0's (or any convenient
symbol) of length n).
Interestingly, "On Computable Numbers" came close to superfluity. When Turing
released his paper, Alonzo Church, a mathematician at Princeton, had recently
published his own solution to the Entscheidungsproblem. Turing's paper
had great significance, though, because of the nature of the mathematical model
of computation that it introduced. Church's approach had been completely
abstract. But the Turing Machine bridges the gap between physical reality and
abstract model. It is a mathematical entity, and yet one speaks of it in terms
of familiar physical parts such as tapes and read/write heads. Babbage would
have appreciated this closing of the gap between engineering and theory.
Many arguments about Turing Machines involve hand-waving because the
mathematical rigour of detailing a Turing Machines's transition function is
drudgery, and nobody likes to do it. This example will be mostly in English,
although there will be some formal notation. A Turing Machine is given a
binary number, in the conventional notation of zeroes and ones, stored on its
tape with the least significant digit on the left and the most significant
digit on the right. (Conventionally, numbers are written in the opposite
direction, with the most significant digit on the left, but since the tape is
bounded on the left, it is easier and makes for a clearer presentation to
extend the number on the right instead of moving everything one cell to the
right and placing the result of a carry on the left.) The Turing Machine must
increment the number, leaving the result on the tape. In this problem it does
not matter whether the Turing Machine accepts or rejects; we are interested
only in the contents of the tape when the machine halts.
What is the information that the Turing machine should remember in its finite
control? The only way that a previous stage of the computation can affect a
later stage is through a carry out of one digit's place and into the next. So
the finite control should remember whether or not it must add in a carry during
the current operation. Two states suffice for this; they can be labelled
"CARRY" and "NO_CARRY".
What should be the initial state? Since the machine must add 1 to its input,
it should begin in CARRY.
Now we reach the most complex part of the design of a Turing Machine, the
transition function. In this example the d function is rather simple. Here is
a table for it:
| STATE | TAPE SYMBOL | ACTION |
|---|
| NO_CARRY | 0 | (NO_CARRY, 0, right) |
| 1 | (NO_CARRY, 1, right) |
| B | undefined; halt when this case is encountered |
| CARRY | 0 | (NO_CARRY, 1, right) |
| 1 | (CARRY, 0, right) |
| B | (NO_CARRY, 1, right) |
This function specifies that whenever the machine is in state NO_CARRY it
should leave the contents of the tape unchanged. (Since there is no way to get
out of NO_CARRY once this state has been entered, we could just as easily have
omitted NO_CARRY altogether and had the machine halt in cases where it would
have entered NO_CARRY.) When the machine is in CARRY and sees a 0 on the tape,
it writes a 1, representing the original 0 with a carry added in, and enters
NO_CARRY. When the machine is in CARRY and sees a 1 on the tape, there will be
a carry into the next column, so it writes a 0 and stays in CARRY. If the
machine sees a blank while it is in CARRY, this means that there is a carry out
of the last column, and the number becomes one digit longer. In this case, the
blank is replaced with a 1.
During the war Turing was involved in the secret effort of the Government Code
and Cipher School to break the German "Enigma" code. The code was generated by
a simple mechanical computer consisting of rotors and plugboards. Turing was a
godsend for the British war effort, and this intense, prolonged intimacy with
coding was beneficial in his later development of electronic stored-program
computers. Turing and other members of the deciphering effort designed
electromechanical devices to step through combinations and detect possible
Enigma encodings. These machines, along with the Enigma device which they were
designed to defeat, were a link between the mechanical computing "engines" of
Babbage and the purely electrical machines that were to appear after the war.
At the end of the war, Turing joined the staff of the National Physical
Laboratory, and wrote a proposal for the construction of an electronic
computer. The proposed machine was dubbed ACE, an acronym for "Automatic
Computing Engine", in recognition of Babbage's Analytical Engine. Other teams
in Britain and in the United States were also at work on electronic
stored-program computers. Unlike Babbage's machines, these would use the same
memory for both data and instructions. Whereas Babbage's machines continually
read their instructions from punched cards and used their internal memories
only for representing the numbers to which the program was referring,
stored-program computers take advantage of the fact that a program can be
viewed as nothing more than a sequence of numbers. If a number, an instruction
code, is assigned to each operation that the machine can perform, then a
program, which is a sequence of operations, reduces to a numerical sequence.
In fact, programs and data become interchangeable. This presents the
delightful possibility of programs that rewrite themselves, or programs that
write other programs.
When I was first learning assembly language, on an old 8-bit microprocessor
with 16-bit pretensions, the Motorola 6809, one of my favourite tricks was
this:
ENTRY: CMPX #$8603
...loop body... BNE ENTRY+1
In this instance, what I wanted was a loop in which a register, A (In case you
know nothing about computer architecture, a register can be thought of as just
a special kind of variable), would be loaded with the value 3 at the beginning
of every iteration but the first, but would have its value preserved on the
first iteration. So I hid the code for the "A := 3" instruction ("LDA #$03" in
6809 assembly language) inside the operand of a harmless instruction, CMPX#,
which, in the context of this loop, had no significant effect. So, when the
processor entered the loop and began the first iteration, it would execute the
harmless instruction, skip over the "A := 3" that was hidden in the operand of
that instruction, and therefore leave the contents of A undisturbed. But, the
branch instruction at the bottom of the loop, which tells the processor what
point to return to to begin the next iteration, points to a location one byte
past the CMPX#. (ENTRY is the label of the CMPX# instruction, so ENTRY+1
points just past the code for the CMPX# in memory.) So now the machine treats
what was previously an operand as an instruction code! It sees $86 (`$'
indicates a base-sixteen number), and treats that as the code for the
instruction LDA#, which takes a one-byte operand, in this case 3. Babbage's
machine would never have been able to perform this sort of devilish trick. It
used separate streams of cards for data and for instructions, and so could not
interchange them. This is a small example of the sort of ingenious finagling
that the programmers and operators of the first electronic stored-program
computers puzzled over every day. By finding creative ways to represent
information inside a computer memory, they could make their machines sing the
music of the spheres.
The first one of these machines to operate was constructed at Manchester
University. It used luminous dots written on cathode ray tubes (CRT's, merely
black-and-white television screens) for storing its instructions and data. The
only output mechanism was the primitive one of peeking at the CRT's and viewing
their patterns of dots as the binary data inside the machine's memory. If you
have ever played with graphics on a microcomputer then you can understand the
simple delight of this: there on the screen was a window into the essence of
the machine's computation. What appeared to the eye as random splotches of
light and dark was known by the intellect as the carrier of all the information
of the problem that the machine had been programmed to solve. One of the first
things I did with my old 6809 system when I learned how to program its graphics
hardware was to write a short routine that set the graphics hardware to display
the program and the data that it was modifying. So on the screen, as light and
dark spots, appeared the instructions and data of the very program that had
issued the command that caused the screen to display it. This delightful
little circularity conveys the beauty of encodings and ciphers.
Ironically for one so aware of the omnipresence of systems, Turing was
maltreated by the system of English society. Turing was homosexual, and when
he inadvertently revealed to the police that he had had homosexual intercourse
he was arrested and charged with the crime of "gross indecency". He was
compelled to submit to injections of oestrogen, a female sex hormone that was
thought to be a remedy for his "disease". After he had served this sentence,
when he seemed to have passed the nadir, he killed himself by eating an apple
laced with cyanide. He left no explanation for his suicide, at least not
explicitly. The explanation lies encoded somewehere within the story of
Turing's life. Hugh Whitemore, author of the biographical play Breaking the
Code, believes that Turing's suicide was the ultimate experiment in
artificial intelligence. In his famous article "Computing Machinery and
Intelligence" in the British philosophical journal Mind, Turing had
discussed the idea of a deterministic machine simulating human behaviour. If,
he said, the machine could not be distinguished objectively from a human, then
one would have to credit it with intelligence. This raises the existential
question of whether or not humans are biological automata, whether death is the
condition of a machine halting. Can mind exist without body? If so, in what
manner? Turing had been fascinated by this since his childhood. He could find
his answer only by first-hand experience. If this was not the primary
motivation for Turing's suicide, it must at least have been in his mind when he
bit into the apple. Turing's death served a dual purpose: it was an escape
from social systems as well as a way of possibly answering the mind-body
question. Since the end of the war, Turing had been under pressure not only
because of his homosexuality, but also because of his way of learning about the
world. The academic system within which Turing was operating enforced a
duality of pure science and engineering. The administrative entities within
which Turing was placed were organised around this division between theory and
application, so Turing was pressured, not so much by any individual
administrators as by the administrative system, to be either a theorist or an
implementor, but not both. This was contrary to his nature and must have been
uncomfortable for him.
EXERCISE
Suppose that a Turing Machine constructor produces defective Turing Machines.
In these machines, whenever the finite control calls for the head to move left,
the head sticks where it is. What kind of languages is accepted by these
machines? Why?
Extensions to Turing Machines
There are many bells and whistles that can be added to Turing Machines that
simplify their construction by hiding the nitty-gritty details. However, none
of them constitute an increase in computing power over the capability of the
basic Turing Machine, because all these extensions can be simulated on a basic
Turing Machine.
One useful extension is the multiple-track Turing Machine. On a Turing
Machine with k tracks, k symbols at a time are under the
read/write head. A basic Turing Machine with tape alphabet 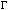 '
can be viewed as a multi-track Turing Machine with tape alphabet
'
can be viewed as a multi-track Turing Machine with tape alphabet 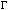 .
The key is to pack a column of k symbols of the alphabet of the
k-track Turing Machine into one symbol of the alphabet of a basic Turing
Machine. The elements of
.
The key is to pack a column of k symbols of the alphabet of the
k-track Turing Machine into one symbol of the alphabet of a basic Turing
Machine. The elements of 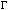 ' will be k-vectors
[a0, a1, ... ak-1] of the elements of
' will be k-vectors
[a0, a1, ... ak-1] of the elements of 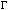 . No
changes or fancy encodings need to be made in states or transitions, because
the k-track machine has only one read/write head and thus cannot treat
symbols that are all in one column independently. There are examples in human
languages of two symbols being treated as a single symbol. Although these
symbols seldom occur in Modern English, Old English used the symbol "æ"
to represent the vowel sound in "mat", for example. This is reminiscent of the
encoding of names of states that was used in the subset construction.
. No
changes or fancy encodings need to be made in states or transitions, because
the k-track machine has only one read/write head and thus cannot treat
symbols that are all in one column independently. There are examples in human
languages of two symbols being treated as a single symbol. Although these
symbols seldom occur in Modern English, Old English used the symbol "æ"
to represent the vowel sound in "mat", for example. This is reminiscent of the
encoding of names of states that was used in the subset construction.
A multi-tape Turing Machine is a generalisation of the multi-track Turing
Machine. It has k tapes, each with its own independently mobile
read/write head. Such a machine can be easily simulated by a 2k-track
machine, and therefore by a basic machine. Each tape is implemented with two
tracks. One of these tracks contains the contents of the tape. The other
contains all blanks except for a single non-blank symbol. This symbol marks
the position of the read/write head for the tape. The transition function
manipulates the contents of the data track and moves this marker symbol along
the marker track in accordance with the actions of the k-tape machine
being simulated. (Yes, this argument is hand-waving. I warned you.)
A machine with a tape that extends infinitely in both directions can be
simulated by a 2-track machine. There is a nice image for this simulation: the
two-way infinite tape is snapped at its origin, and half of it is rotated in a
semicircle to match up with the other half. There is one track for each half
of the tape. But why stop at a recording surface (or a recording solid, or a
recording hyper-solid) that is infinite only in one dimension? If the tape[45] is an infinite plane, an infinite solid, an infinite
object in a space of any number of dimensions, then it still can be simulated
using the one-dimensional, semi-infinite tape of the basic Turing Machine.
This is because any such multi-dimensional tape that is divided into cells
contains the same infinite number of cells as a one-dimensional, semi-infinite
tape. (Specifically, they both have 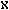 0 cells.) They may be more
immediately accessible in higher dimensions, but they are all still there and
are accessible, given enough time for the read/write head to move, in a tape of
any dimension. To understand why this is so, see the appendix on infinity.
All that needs to be done is to define some arbitrary one-to-one mapping
between the
0 cells.) They may be more
immediately accessible in higher dimensions, but they are all still there and
are accessible, given enough time for the read/write head to move, in a tape of
any dimension. To understand why this is so, see the appendix on infinity.
All that needs to be done is to define some arbitrary one-to-one mapping
between the 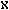 0 cells of one tape and the
0 cells of one tape and the 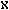 0 cells of the other
and then implement that mapping in the finite control of the one-dimensional
Turing Machine. You should take a moment to understand how this simulation can
be combined with the previous one to simulate a machine with k two-way
infinite tapes (or k multi-dimensional tapes) using a 4k-track
machine.
0 cells of the other
and then implement that mapping in the finite control of the one-dimensional
Turing Machine. You should take a moment to understand how this simulation can
be combined with the previous one to simulate a machine with k two-way
infinite tapes (or k multi-dimensional tapes) using a 4k-track
machine.
One naïve objection to the statement that Turing Machines can do anything
that real-world computers can do is "they can't do graphics". This is untrue.
Of course if a basic Turing Machine were actually a physical construction it
would not have the display hardware necessary to output graphics in a visual
form. But a graphics display is only one physical way of regarding the
abstract mathematical construct of points in a coördinate system. A
Turing Machine is capable of computing such points. Therefore, minus the fancy
displays, Turing Machines can do graphics. Think of a Cartesian (i.e.
rectilinear) coördinate system. It can be represented using 1's and 0's
on a two-dimensional recording surface of a Turing Machine. If a point can be
one of several colours, then instead of just 1's and 0's we can have a symbol
for each possible colour. In general, a Turing Machine can do graphics in any
coördinate system (polar, cylindrical, or spherical, for example) and in
any number of dimensions by simulating a tape of the desired number of
dimensions that has its cells laid out according to the desired coördinate
system.
As was the case with finite automata, nondeterminism does not add any
computing power to the Turing Machine. A deterministic Turing Machine is
capable of simulating every case in which a nondeterministic Turing Machine
might find itself. The deterministic machine can allocate separate areas on
its tape for each case. Whenever a nondeterministic choice is encountered, a
new data area is created. When there is no more room in a data area, all the
areas stored to the right of it on the tape are shifted right to make more
room. There is the possibility that one of the simulations might not halt but
instead enter an endless loop. We will see shortly that there is no algorithm
to detect whether an algorithm can ever get into an endless loop, so this case
cannot be anticipated. If the cases were simulated sequentially, with the
simulating machine completing one case before embarking upon the next, then a
nonterminating case would prevent the simulator from ever proceeding to the
next case. Therefore, the simulator must be time-shared between all the cases
of the simulation. The simulator is a loop that visits each case once on each
pass. On each visit, one move is accomplished. With this arrangement,
infinite loops cannot monopolise the simulator.
EXERCISES
In the problems that follow, remember not to get too nitty-gritty in your
descriptions.
- 0. Describe a Turing Machine that implements the Russian Peasant multiplication
algorithm, discussed in the section on proving loops correct. You may assume
any convenient format for your input and output strings, but be sure to specify
what that format is.
- 1. To provide a counterexample for those less well informed than yourself who
claim that Turing Machines can't do graphics, design a Turing Machine that
plots linear equations in the Cartesian plane. The input will be in the form
of two binary numbers (b, c) on an input tape, separated by an `X'. The
output is on a flat recording surface with boundaries at x=-100,
x=100, y=-100, and y=100. The machine should plot every
pair of integers on this surface that lies on the line y =
bx+c. (Obviously, in this scheme you can't plot the fractions
that lie on this line.) Plotting a point consists of changing the
corresponding tape symbol from a blank to an `X'. The head starts out at
position (0, 0) on the plotting surface.
Turing Machine Encodings and the Universal Turing Machine
Turing machines can be encoded as strings. States and symbols can be assigned
numbers. Since symbols can be assigned numbers, and a machine with tape
alphabet 0, 1, B can represent any number (in unary, using 1 as a
delimiter between numbers) using these symbols on its tape, a Turing Machine
with tape alphabet 0, 1, B can simulate any Turing Machine. Therefore
the following discussion can and will be restricted to such machines. A
template for the encoding of a transition could be
<state>1<symbol>1<nonfinal/final><state>1<symbol>1lt;left/right>
where the "<state>" and "<symbol>" templates represent state and
symbol numbers in unary, "<nonfinal/final>" represents either 0, if the
following state code designates a nonfinal state, or 1, if it represents a
final state, and "<left/right>" represents either 0 for left or 1 for
right. There are many other encodings that would work as well; this is an
arbitrary choice. The 1's in the template are delimiters. Since we have
already used a supermarket example, in describing nondeterminism, we shall use
another here. The plastic sticks that are placed between different customers'
purchases at a supermarket checkout serve the same function as the 1's that we
are placing between individual codes in this Turing Machine encoding scheme.
They mark the end of one order (or the end of one code) and the beginning of
the next. A transition function can be encoded as a concatenation of
transition encodings. Note that in order to encode a Turing Machine, all one
must do is encode its transition function, since the input alphabet and the
tape alphabet are fixed as 0, 1 and 0, 1, B, respectively, and the
states are defined implicitly by their occurrences in the transition function.
The initial state can be designated by assigning it the special code of zero.
(In unary, this code would be represented by  , the string of 0's of
length zero.) This encoding of a Turing Machine M can be denoted
e(M), viewing e as an encoding function. So that e can be
defined for all strings of 1's and 0's, we can define any string of 1's and 0's
that does not match the above format to be an encoding of the Turing Machine
that has no states. We now have a method of putting all the information about
a Turing Machine into a string. And strings can be used as data for Turing
Machines. This suggests interesting possibilities.
, the string of 0's of
length zero.) This encoding of a Turing Machine M can be denoted
e(M), viewing e as an encoding function. So that e can be
defined for all strings of 1's and 0's, we can define any string of 1's and 0's
that does not match the above format to be an encoding of the Turing Machine
that has no states. We now have a method of putting all the information about
a Turing Machine into a string. And strings can be used as data for Turing
Machines. This suggests interesting possibilities.
The Universal Turing Machine takes as its input a Turing Machine
encoding and another string. It simulates the specified machine with this
string as its input. The universal machine uses three tapes: one to store the
encoding of the machine being simulated, one to store the current state of the
simulation, and one to store the contents of the tape of the machine being
simulated. Note that the tape that stores the encoding is read-only, because
the encoding is never modified. On each step of the simulation, the universal
machine looks up the proper move for the current combination of state and tape
symbol, and alters the state and the tape contents of the simulation
accordingly. A universal Turing Machine, compared with a special-purpose
Turing Machine, is like a general-purpose, programmable computer in comparison
with a dedicated system. A common type of dedicated system in the real world
is the word processor. Such a computer can edit pieces of text, but it cannot
be programmed to do anything else. A general-purpose computer can simulate any
special-purpose computer. In particular, it can simulate a word processor by
executing a text-editing program. We can denote a Turing Machine M when
run on an input string x as M[x]. Call the Universal Turing
Machine U. Then for any Turing Machine M and any string x,
U[<e(M), x>] yields the same result as M[x] does.
The Halting Problem: An Undecidable Problem
Note that in some cases a Turing Machine may neither accept nor reject, but
instead may loop infinitely. A finite automaton cannot loop infinitely,
because eventually it must reach the end of its input. But giving the Turing
Machine the power to rewrite its input also gives it the capability of looping
infinitely. It is desirable to produce Turing Machines that halt on all
inputs, just as it is desirable to produce computer programs that can never
enter infinite loops. A Turing Machine that halts on all possible inputs is
called a total Turing Machine. Turing Machines that are not total may
halt on some of their inputs, but waiting for a nontotal Turing machine to halt
is a never-ending task; one can never be sure if the machine is still doing
useful computation and might halt even within the next few transitions or
whether it has entered an infinite loop. (You may have had the experience of
sitting in front of a computer that seemed to be taking a long time to finish
and wondering whether or not you should interrupt it and see whether it had
entered an infinite loop.) If a language is accepted by some total Turing
Machine, the language is termed recursive. (The meaning of the word
"recursive" in this domain should not be confused with its meaning in the
domain of program implementation strategies; although recursive sets and
recursive programs do bear a close relation, it can be confusing for beginning
students.) One might think that every language is recursive, that is, that
every well-defined problem can be solved by a computer. In this case,
obtaining the solution would simply be a matter of constructing a correct
algorithm. But there are many interesting problems that cannot be encoded as
recursive languages. These problems are undecidable.
A problem A is reducible to another problem B if and only
if there is a recursive function that maps instances of A to instances
of B. The statement "A is reducible to B" is denoted A
<= B. This `<=' notation arises from the notion of a
hierarchy of problems; problems higher up in the hierarchy are more difficult
than problems lower down, and any given problem is reducible to problems that
are as hard or harder. Thus `<=' defines a classification of problems in
terms of difficulty.
We want to know whether it is possible to design an algorithm that takes as
its input another algorithm and the input to that algorithm, and decides
whether or not the given algorithm will ever halt after it has been set running
on the given input. In Turing Machine terms, we want a machine H that,
when given <e(M), x> for any Turing Machine M and any
string x, will accept if and only if M would eventually halt
(i.e., accept or reject) if run on x, and reject otherwise. A good way
to see if such an algorithm can exist is not to go through all the trouble of
trying to construct it but instead to assume that it exists and then to see if
its existence implies a contradiction. If its existence does imply a
contradiction, then it cannot exist, and we need not bother to try to construct
it. This method of proof by contradiction is called indirect proof. It
may be familiar to you from geometry. So suppose H exists. Then we can
construct from H a machine M* that behaves
as follows. When run on a string over 0, 1 that is e(M) for some M
(remember that e is defined for all strings over 0, 1), M*
simulates H[<e(M), e(M)>] and
* halts iff M[e(M)] does not halt
* loops endlessly iff M[e(M)] halts
This simulation of H decides whether or not M halts when given
its own encoding as input. In a mind with an intuition for paradox,
this raises the question of what happens when M*
is given its own encoding as input. Think it through for yourself using the
definition of M*, then read on.
What we have is a contradiction. M*[e(M*)]
halts if and only if it does not halt, and does not halt
if and only if it halts. (Therefore, the moon is made of green cheese.) So we
must have made some false assumption. Note that L(M*)
is reducible to L(H). The recursive function
that maps elements of L(M*) to elements of
L(H) is implemented in the above-mentioned modifications to the
transition function of H. We made no assumption in the construction of
M* from H; that process is perfectly
well-defined. The only assumption that has been made is that H exists;
the only way that M* cannot exist is if H,
the machine on which it is based, also cannot exist. Therefore there is no
algorithm for the halting problem; the question of whether or not any given
algorithm halts on any given input is provably undecidable.
EXERCISES
- 0. Describe the proof of the undecidability of the Halting Problem in terms of
your favourite computer language. That is, instead of machines, speak about
subroutines. Show that it's impossible for a subroutine H, which
decides whether or not its parameter M halts, to exist. (For example,
in Pascal, assume that there is a function H that takes a parameter of
type PROGRAM and returns true if that program halts on all inputs and false
otherwise. Use H to define a Pascal function that behaves like
M* above.)
- 1. Is it possible to write a Pascal program that tells whether or not any given
program will print anything when executed? Explain.
- 2. Is it possible to write a Pascal program that tells whether or not any given
program ever calls some particular procedure? Explain.
A Taste of Gödel's Incompleteness Theorem
"Logic dictated that logic did not apply." This was the statement used by
Mister Spock in a Star Trek episode to give logical justification to an
action that seemed the product of illogic[46]. It is also
an informal statement of a logical truth first proven by Kurt Gödel in
1931. At that time mathematics had been trying to set its own house in order
ever since the days of the Cambridge Analytical Society. There had been too
many loopholes that had arisen through lack of rigorous demonstrations of
mathematical truths, and it had taken about a century to clean them up. By the
early twentieth century mathematicians were searching for the pièce
de résistance of mathematical rigour, a proof of the consistency and
completeness of mathematics. Consistency of a mathematical system means
that it is impossible to use the axioms and inference rules of the system to
prove anything that is false. Inconsistent mathematical systems are not of
much use, because mathematics is boring when, like the Bellman, one can prove
anything that one wants to prove. Completeness means that it is
possible to prove every true proposition that can be expressed within the
syntax and semantics of the system. Obviously, completeness is a desirable
property, for when one is trying to come up with a proof of a conjecture that
seems true, one would like to be assured that one is not on a wild goose chase.
But Gödel showed that any mathematical system with enough expressive power
to encompass number theory is necessarily incomplete or inconsistent. This
proof is one of the most famous and one of the most valuable demonstrations of
the old saw that you can't have your cake and eat it too.
Gödel accomplished his proof by encoding mathematical symbols using
numbers, in a scheme called Gödel numbering, and then using this encoding
to construct a mathematical proposition that, when decoded, expresses a
mathematical equivalent of the English sentence "This statement cannot be
proven". The coding is what allows the self-reference of such a statement; it
can talk about itself on two levels, within the code and outside the code. The
proposition must be either true or false. If it's true, then, as it declares,
it can't be proven. In this case the mathematical system that generated this
statement is incomplete, since the statement is an example of a proposition
that is true and yet has no proof within the system. If it's false, then it
can be proven, which means the system is inconsistent, since the statement is
an example of a false proposition that has a proof within the system.
We can construct a Turing Machine E to enumerate theorems in any formal
system by successively applying inference rules to statements already known to
be true. Eventually, any given theorem will be enumerated by such a machine.
(Of course, most of the theorems will not be interesting, but the interesting
ones will all be there. This is like the old story about the monkeys at the
typewriters eventually producing the complete works of Shakespeare, or the
situation in Borges's Library of Babel.) We can use E to create a
machine called G that has the following behaviour: G simulates
E. If and when this simulation of E produces a theorem that
states that G does not halt, G halts. Think about the
implications of this construction for the consistency and completeness of the
system whose theorems are enumerated by E, then read on.
If G halts, then the formal system whose theorems it has been
enumerating is inconsistent, because the statement that G does not halt
is provable but untrue. If G does not halt, then the system is
incomplete, because it generates no proof that G does not halt. An
adversary to this argument might say, "Well, if my mathematical system can't
express the fact that G never halts, then I'll just add that fact
explicitly, as an axiom". This would be like trying to plug one small hole in
a disintegrating dyke: another leak will automatically spring up. For in
adding this axiom to the system, the adversary has changed the system, so the
original enumeration machine no longer applies. We now need a slightly altered
machine, E', to enumerate theorems in this new system. We can use this
new enumeration machine to construct a machine G', and we will find that
the new system is still incomplete, because it fails to include as a theorem
the true statement that G' never halts. Thus, whenever the adversary
attempts to wriggle out from under the effects of the Incompleteness Theorem,
he is easily caught again. You should be aware that this is only a quick,
hand-waving argument. The complete, mathematically rigorous Incompleteness
Theorem is a gem, an opus.
Gödel's Incompleteness Theorem is the capstone to the wave of
mathematisation begun by Newton. It shows that there is a limit; mathematics
cannot encompass all truth. This has been reassuring to humanists. It has
reassured me of the purpose in my nonmathematical work. If, as the western
scientific tradition suggests, the universe really is nothing but a
mathematical system, then anything that happens, including all thought, must be
expressible in terms of number theory. Can it be so? This is what Turing was
trying to decide when he bit into the apple. If this question is ever decided,
a very fundamental harmony will have been revealed. But humans will not be
able to say that they have found the key to all truth. For if the universe is
simply a mathematical system, then it contains truths that cannot be reached
using logic. What might such unprovable truths be? The enlightenments of Zen,
perhaps? When I first studied formal logic I was filled with the same joy that
filled the Newtonian mathematisers: everything could be reduced to symbol
manipulation, I thought; it was feasible that eventually there would be no need
for the messy ambiguities of literature and philosophy. How narrow-minded and
ignorant that sentiment was! I thought that I had a logical reason to abandon
the humanities when, in actuality, logic was saying exactly the opposite.
NEXT CHAPTER: 3. Conclusion
[26][Carroll 1936] p. 17.
[27][Carroll 1936] p. 761.
[28][Carroll 1936] p. 769.
[29][Carroll 1936] p. 757.
[30][Carroll 1936] p. 770.
[31][Carroll 1936] p. 774.
[32][Atherton 1960]
[33][Joyce 1939] p. 374.
[34][Carroll 1936] p. 124.
[38]David Gries, in an electronic message to the Cornell
University Department of Computer Science dated March 9, 1989. Used by
permission.
[39][Morrison] p. 143.
[40][Morrison] p. 252. Ada's notes on Menabrea.
[41]The Golden Age ended sometime in the early 1980's, and
now the media have popularised the word "hacker" as a term for one who
maliciously enters and damages computer systems to which they do not have
access. This is unfortunate.
[42]William Whewell, Astronomy and General Physics,
Considered with Reference to Natural Theology 1/e. London: William
Pickering, 1833. p. 334.
[43][Babbage 1838]
[44]The proofs in this section appear in [Hopcroft &
Ullman 1979].
[45]I use the word "tape" here, for lack of a concise
substitute, to designate a recording material of any number of dimensions.
[46]The episode was "The Galileo Seven".
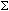 '. A
string over an alphabet is a finite sequence of symbols from the
alphabet. A symbol by itself is a string whose length is one. The
length of a string is the number of occurrences of symbols in the
string. The length of a string x is denoted by `|x|'. The
null string is the special string that contains no symbols (i.e., its
length is zero). It is represented by `
'. A
string over an alphabet is a finite sequence of symbols from the
alphabet. A symbol by itself is a string whose length is one. The
length of a string is the number of occurrences of symbols in the
string. The length of a string x is denoted by `|x|'. The
null string is the special string that contains no symbols (i.e., its
length is zero). It is represented by ` '. String variables are
usually represented by the letters u, v, w, x, y, z, and symbol
variables are usually represented by a, b, c, .... The
concatenation operation joins two strings. It is similar to
append in the lists world and to . in Peano arithmetic. Concatenation,
like multiplication in arithmetic, is symbolised either by juxtaposing two
variables and omitting the operator, as in `xy', or by the operator `.',
as in `x.y'. As nil is the identity element for append in
the lists world,
'. String variables are
usually represented by the letters u, v, w, x, y, z, and symbol
variables are usually represented by a, b, c, .... The
concatenation operation joins two strings. It is similar to
append in the lists world and to . in Peano arithmetic. Concatenation,
like multiplication in arithmetic, is symbolised either by juxtaposing two
variables and omitting the operator, as in `xy', or by the operator `.',
as in `x.y'. As nil is the identity element for append in
the lists world,  is the identity element for . in the strings
world. A substring is a string that is part of another string, that is,
string x is a substring of string y if and only if there exist
strings u and v such that y=uxv. u or v or
both may be the null string, in which cases, respectively, x is said to
be a prefix of y, a suffix of y, or simply y.
A string x superscripted with a natural number n represents
x repeated n times: a5 = aaaaa. So a
superscript n is shorthand for n-1 concatenation operations.
(n-1 concatenations, not n of them, because to repeat a string
only once does not require a concatenation; it requires only writing out the
string.) This was the origin of our meta-notation for strings of `s's in Peano
arithmetic. The superscript 0 is defined, following Peacock's Principle of the
Permanence of Equivalent Forms, as producing
is the identity element for . in the strings
world. A substring is a string that is part of another string, that is,
string x is a substring of string y if and only if there exist
strings u and v such that y=uxv. u or v or
both may be the null string, in which cases, respectively, x is said to
be a prefix of y, a suffix of y, or simply y.
A string x superscripted with a natural number n represents
x repeated n times: a5 = aaaaa. So a
superscript n is shorthand for n-1 concatenation operations.
(n-1 concatenations, not n of them, because to repeat a string
only once does not require a concatenation; it requires only writing out the
string.) This was the origin of our meta-notation for strings of `s's in Peano
arithmetic. The superscript 0 is defined, following Peacock's Principle of the
Permanence of Equivalent Forms, as producing  , the identity element
for ..
, the identity element
for ..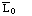
 L1
L1 L1
L1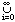 Li. For example, {a, b, c}*
= {
Li. For example, {a, b, c}*
= {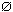 is a regular expression representing
is a regular expression representing 

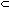 L(0*1*0*)
L(0*1*0*)
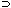 L(1*+0*)
L(1*+0*)
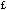 17,000 spent on the Difference Engine by the British
government was well disposed even without the completion of the project,
because of the advances in the state of the art of mechanical engineering that
accompanied the development of the Difference Engine. (This same argument is
now employed to justify spending by the Department of Defense in the United
States.) Babbage's nineteenth-century universe was still the mechanistic one
of Newton, so he never could have conceived a physical implementation of a
computing device as anything but a mechanism, an arrangement of gears, springs,
and levers. The developments in the study of electromagnetism which were to
lead to the genesis of electronics did not occur until the latter part of the
nineteenth century.
17,000 spent on the Difference Engine by the British
government was well disposed even without the completion of the project,
because of the advances in the state of the art of mechanical engineering that
accompanied the development of the Difference Engine. (This same argument is
now employed to justify spending by the Department of Defense in the United
States.) Babbage's nineteenth-century universe was still the mechanistic one
of Newton, so he never could have conceived a physical implementation of a
computing device as anything but a mechanism, an arrangement of gears, springs,
and levers. The developments in the study of electromagnetism which were to
lead to the genesis of electronics did not occur until the latter part of the
nineteenth century. :
:
 . Saying that a finite automaton
accepts
. Saying that a finite automaton
accepts 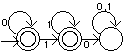
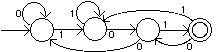
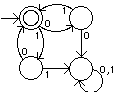
 .
Since the transition function in an NFA maps into the
power set of the set of states, the result is a set of states instead of a
single state. From this set the machine chooses a next state. Because of the
nondeterminism, there may be paths labelled with the input string that end on
nonfinal states as well as ones that do end on final states. The path is
chosen in such a way that if there is any path that terminates on a final
state, it will be the path selected. If there is more than one such path
terminating on a final state, the particular choice of path does not matter.
.
Since the transition function in an NFA maps into the
power set of the set of states, the result is a set of states instead of a
single state. From this set the machine chooses a next state. Because of the
nondeterminism, there may be paths labelled with the input string that end on
nonfinal states as well as ones that do end on final states. The path is
chosen in such a way that if there is any path that terminates on a final
state, it will be the path selected. If there is more than one such path
terminating on a final state, the particular choice of path does not matter. . If you start with an eight-state NFA, that's only 256
states! (Fortunately, the actual number of states produced by the subset
construction is usually much less than this exponential upper bound.) We
continue in the construction by computing the outgoing transitions of the new
state [INIT, ZERO_1].
. If you start with an eight-state NFA, that's only 256
states! (Fortunately, the actual number of states produced by the subset
construction is usually much less than this exponential upper bound.) We
continue in the construction by computing the outgoing transitions of the new
state [INIT, ZERO_1]. 
 ,
, 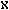 0 cells.) They may be more
immediately accessible in higher dimensions, but they are all still there and
are accessible, given enough time for the read/write head to move, in a tape of
any dimension. To understand why this is so, see
0 cells.) They may be more
immediately accessible in higher dimensions, but they are all still there and
are accessible, given enough time for the read/write head to move, in a tape of
any dimension. To understand why this is so, see